[Linear Algebra] 변환(Transform): 핵 그리고 치역(Kernel and Range)

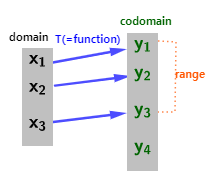
핵과 치역(Kernel and Range)

변환은 어떤 수 x를 식에 대입하여 그 값에 대응하는 결과인 y를 반환하는 함수를 의미합니다. 다시 말하면 어떤 값들에 함수를 적용하여 변환된 결과가 생성되는 과정을 변환(transforamtion)이라 합니다. 이 과정에서 함수를 기준으로 입력된 데이터의 범위를 정의역(domain)이라하며 이에 대응하는 가능한 모든 결과물들의 범위를 공역(codomain)이라고 합니다. 예로서 python에서 함수 int()는 실수를 정수로 만들기 위해 사용합니다. 이 경우 정의역은 실수이지만 공역(codomain)은 정수가 될것입니다.

x=3.24
y=int(x)
y

3

공역 중 함수의 결과를 상(image)이라 하며 이 상들의 집합을 치역(range)이라고 합니다. 치역(range)은 공역의 부분집합이 됩니다.

식 1의 선형결합은 표준행렬에 의해 변수벡터의 변환된 결과를 나타내는 것으로 위에서 소개한 변환과정으로 나타낼 수 있습니다. 즉, 변수벡터와 결과는 각각 정의역과 치역이 되며 이들의 매개가 되는 표준행렬은 함수로 간주할 수 있습니다.

\begin{align}\begin{bmatrix}-2& -1\\0& 4 \end{bmatrix}\begin{bmatrix}3\\1\end{bmatrix}&=\begin{bmatrix}-7\\-4\end{bmatrix}\\ F(\text{정의역})&=\text{상}\end{align}

(식 1)

식 1의 표준행렬을 함수 F()로 표시하였습니다. 일반적으로 위와 같은 결합에서 함수는 Transform의 접두어를 적용하여 T()로 나타냅니다.

그림 1은 정의역, 공역, 그리고 치역을 나타낸 것입니다.

그림 1. 정의역(domain), 공역(codomain), 그리고 치역(range).

함수에 의한 정의역과 공역의 대응은 그림 2와 같이 정의할 수 있습니다.

그림 2. 정의역과 공역의 대응방식.

변환의 종류

• 단사(Injective, one-to-one)
  • 정의역과 공역의 일대일 대응. 그림 2(a)와 (c).
• 전사(Subjective, onto)
  • 치역 = 공역, 그림 2(b)와 (c).
• 전단사(Bijective)
  • 일대일 대응이면서 공역(codomain)과 치역(range)이 같은 경우. 그림 2(c).

예 1)

행렬 A에 대한 상이 b일 경우 정의역 x를 결정합니다.

\begin{align}T: \mathbb{R}^3 \rightarrow \mathbb{R}^3,\; T(x)&=Ax=b\\\begin{bmatrix}4&4&2\\12& 15& 5\\-8& -17& 4 \end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}&=\begin{bmatrix}-4\\-11\\15\end{bmatrix}\end{align}

식에서 함수 T인 표준행렬 A의 경우 정방행렬이므로 역행렬의 존재 여부로 선형독립을 판단할 수 있습니다.

A=np.array([[4,4,2],[12, 15, 5], [-8, -17, 4]])
b=np.array([-4, -11, 15])
la.det(A).round(3)

60.0

A의 행렬식은 0이 아니므로 역행렬을 가집니다. 즉, 위 선형시스템은 독립이므로 numpy.linalge.solve() 함수를 사용하여 해 벡터를 결정할 수 있습니다.

sol=la.solve(A, b)
print(sol)

[-3.  1.  2.]

결과인 해벡터는 위 시스템의 정의역이 됩니다.

선형결합은 표준벡터에 따른 변환 결과들의 합과 스칼라 배수에 대해 성립합니다. 이러한 성립은 식 2와 같이 변환(함수)에 대해 나타낼 수 있습니다.

T(x1) + T(x2) = T(x1 + x2)	[덧셈]	(식 2)
s·T(x) = T(s·x), s: scalar	[스칼라배수]

이 선형결합은 표준행렬을 통해 좌표벡터를 결과벡터로 변환시키는 것으로 선형변환(linear transfomation)이라 합니다. 다시말하면 선형변환은 선형결합이 성립하는 시스템을 나타냅니다. 예를 들어 m × n 형태의 행렬 A에 대해 T(x) = Ax의 선형변환 과정은 식 4.1.3과 같이 나타낼 수 있습니다.

$$\begin{bmatrix}a_{11}& a_{12}& a_{13}\\a_{21}& a_{22}& a_{23}\\a_{31}& a_{32}& a_{33}\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}a_{11}x_1+ a_{12}x_2+ a_{13}x_3\\a_{21}x_1+ a_{22}x_2+ a_{23}x_3\\a_{31}x_1+ a_{32}x_2+ a_{33}x_3\end{bmatrix}$$

(식 3)

위 식의 벡터 x가 정의역이며 우항의 결과가 치역이 됩니다. 정의역의 차원은 행렬 A의 열 차원과 같으며 치역의 차원은 A의 행차원과 같습니다.이러한 선형변환에서 모든 치역의 모든 요소가 0이 되는 정의역을 핵(kernl)라고 합니다. 즉, 동차선형결합(Homogeneous Linear Combination)의 해벡터를 핵이라하며 이러한 선형변환을 식 4와 같이 ker T로 나타냅니다.

ker T = {v ∈ Rn| T(v) = 0}

(식 4)

예 2)

다음은 2차원에서 2차원으로 변환되는 선형변환입니다. 이 선형변환에서 ker T를 위한 조건을 결정해봅니다.

T: ℝ² → ℝ², T(x, y) = T(x - y, 0)

일반적으로 차원(dimension)은 객체를 나타내기 위해 필요한 축으로 수를 의미합니다. 그러나 그러나 ℝ로 표현되는 실수 백터의 차원은 그 벡터를 구성하는 요소의 갯수를 의미합니다.

위 변환을 일으킬 수 있는 표준행렬 즉, 변환인자(T)는 식 5와 같습니다.

\begin{align}T\left(\begin{bmatrix}x\\y\end{bmatrix}\right)&=\begin{bmatrix}1\\0\end{bmatrix}x+\begin{bmatrix}-1\\0\end{bmatrix}y\\ &=\begin{bmatrix}1& -1\\0& 0\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}\\&=\begin{bmatrix}x-y\\0\end{bmatrix}\end{align}

(식 5)

ker T를 위해서는 모든 치역이 0이 되어야 하므로 식 6과 같이 x = y 일 조건을 만족하여야 합니다.

ker T = {(x, y) ∈ℝ2| y = x}

(식 6)

 

전단사(bijective)이면서 동일한 차원에서 이루어지는 변환을 동형사상(isomorphism)이라고 합니다. 다시말하면 동형사상에서는 정의역과 공역(codomain)의 차원이 같습니다.

예 3)

T(x, y) = (y, x) 변환이 ker T일 경우 단사인지를 결정합니다.

\begin{align}T\left(\begin{bmatrix}x\\y\end{bmatrix}\right)&=\begin{bmatrix}0\\1\end{bmatrix}x+\begin{bmatrix}1\\0\end{bmatrix}y\\ &=\begin{bmatrix}0& 1\\1& 0\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}\\&=\begin{bmatrix}0\\0\end{bmatrix}\end{align}

(식 6)

식 6은 선형동차결합입니다. 위 식이 자명한 해를 가진다면 일대일 반응을 의미하는 것으로서 단사입니다.

A=np.array([[0, 1],[1, 0]])
c=np.zeros((2,1))
la.det(A)

-1.0

표준 행렬 A의 행렬식은 0이 아니므로 가역행렬이며 위 시스템은 선형독립입니다. 즉, 자명한 해를 가집니다.

sol=la.solve(A, c)
print(sol)

[[0.]
 [0.]]

위 결과와 같이 정의역의 각 요소에 대응하는 상은 1개입니다. 즉, 일대일 대응으로 단사입니다.

예 4)

다음 변환이 단사인지를 결정해 봅니다.

T: ℝ³ → ℝ³, T(x, y, z) = (x + 2y - z, y + z, x + y - 2z)

식 7은 위 식을 행렬 변환형태로 나타낸 것입니다.

$$T\left(\begin{bmatrix}x\\y\\z\end{bmatrix}\right)=\begin{bmatrix}1&2&-1\\0&1&1\\1&1&-2\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}$$

(식 7)

A=np.array([[1,2,-1], [0,1,1],[1,1,-2]])
la.det(A)

0.0

변환 T는 비가역행렬이므로 선형종속입니다. 이것은 식 7의 결과 벡터를 위한 다양한 해벡터가 존재함을 나타냅니다. 정의역과 치역의 관점으로 나타내면 치역의 각 요소에 대응하는 정의역의 1개 이상의 요소들이 존재함을 의미합니다. 즉, 위 시스템은 단사가 아닙니다.

ker T = 0 시스템에서 단사(injective) ⇔ 유일한 해를 가집니다. 즉, 선형독립입니다.

예 5)

다음 행렬에 의한 정의역과 공역의 대응방법을 결정해봅니다.

\begin{align}&T\left(\begin{bmatrix}x\\y\\z\end{bmatrix}\right)=\begin{bmatrix}x\\y\end{bmatrix}\\ &T=\begin{bmatrix}1&0&0\\0&1&0\end{bmatrix}\end{align}

위 변환은 식 8과 같이 선형결합으로 표현할 수 있습니다.

$$\begin{bmatrix}1&0&0\\0&1&0\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}x\\y\end{bmatrix}$$

(식 8)

식 8은 z의 모든 수에 대해 만족합니다. 즉, 다양한 해가 존재하므로 단사(injective)는 아닙니다. 그러나 식의 수가 해의 수보다 작고 공역(codomian)과 치역(range)이 같으므로 전사(subjective)입니다.

단사와 전단사의 경우 모두 일대일 반응으로 유일한 해를 가져야 합니다. 이것은 변환 즉, 표준 행렬이 가역행렬이어야 함을 의미합니다.

표준행렬 A가 가역행렬일 경우의 특성

• A의 열벡터, 행벡터가 모두 선형독립입니다.
• ⇔ Ax = 0은 자명한 해를 갖습니다.
• ⇔ Ax = b는 유일한 해를 갖습니다.
• ⇔ A는 가역이고 det(A)≠0입니다.
• ⇔ A의 고유값은 0이 아닙니다(λ ≠ 0)
• ⇔ T는 전단사입니다.