[data analysis]로그-노말 분포(Log-normal distribution)

로그-노말 분포(Log-normal distribution)

랜덤변수의 자연로그가 정규분포를 따른다면 랜덤변수 자체는 로그노말(log-normal) 분포를 따른다고 할 수 있습니다.

X (log-normal)	⇒	Y=ln(x) (normal)
Y(normal)	⇒	X=exp(Y) (log-normal)

양수인 연속 랜덤변수 X를 식 1과 같이 나타낼 수 있다고 가정합니다.

$$R_x = \mathbb{R_{++}} \tag{식 1}$$

랜덤 변수 X의 확률밀도함수가 식 2와 같다면 그 변수는 매개변수 $\mu$와 $\sigma^2$를 가지는 로그노말 분포(log-normal distribution)를 따릅니다.

$$\tag{식 2} f_x(X)= \begin{cases} \frac{1}{x\sqrt{2\pi}\sigma}\exp\left(-\frac{1}{2}\frac{(\ln x -\mu)^2}{\sigma^2}\right)& \text{if}\; x \in R_x\\ 0& \text{if}\; x \notin R_x \end{cases}$$

다음 코드는 식 2를 함수로 작성한 것입니다.

def logNormPdf(x, mu, sigma):
    c1=1/(x*np.sqrt(2*np.pi)*sigma)
    c2=np.exp(-1/2*(np.log(x)-mu)**2/sigma**2)
    return c1*c2

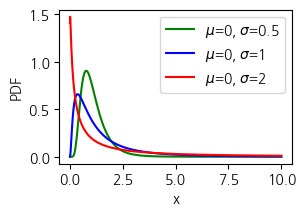
양수인 랜덤변수 x에 대해 모수 중의 σ의 변화에 따른 위 로그-노말 확률밀도 함수를 적용한 행태를 나타냅니다.

x=np.linspace(0.01, 10, 1000)
para=[(0,0.5, 'g'), (0, 1, 'b'), (0, 2, 'r')]
plt.figure(figsize=(3,2))
for i , j, z in para:
    p=logNormPdf(x, i, j)
    plt.plot(x, p, color=z, label=f"$\mu$={i}, $\sigma$={j}")
plt.xlabel("x")
plt.ylabel('PDF')
plt.legend(loc="best")
plt.show()

위 코드의 변수는 로그-노말 분포에 부합합니다. 이 변수에 자연로그를 취한 변형된 랜덤 변수는 정규분포에 부합니다.

y=np.log(x)
pn=stats.norm.pdf(y,scale=0.5/2)
plt.figure(figsize=(3,2))
plt.plot(y, pn)
plt.show()

Y~N(μ, σ²) 즉, 랜덤변수 Y는 μ와 σ²를 모수로 하는 정규분포를 따릅니다. 이 변수에 식 3이 성립하면 랜덤변수 X는 μ와 σ²를 모수로 하는 로그-노말 분포를 따르며 그 확률밀도 함수는 식 4와 같습니다.

$$\tag{식3} X=\exp(Y) \Leftrightarrow \ln X=Y$$

위 식 3에 부합하는 X의 확률밀도 함수는 식 4와 같습니다.

$$\begin{align}\tag{식 4} f_y(y)&=\frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(y-\mu)^2}{2\sigma^2}\right)\\& x=g(Y)=\exp(Y) \\ f_x(x)& =f_y(g^{-1}(x))\frac{dg^{-1}(x)}{dx}\\ &g^{-1}(x)=\ln x \\\ &\frac{dg^{-1}(x)}{dx}=\frac{1}{x}\\ f(x) & =f_y(g^{-1}(x))\frac{dg^{-1}(x)}{dx} \\ & =\frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)\frac{1}{x}\end{align}$$

식 4는 랜덤변수의 Y와 X의 역함수 관계를 적용한 것입니다(증가 확률함수의 역함수 참조).

기대값

로그 노말 분포를 따르는 랜덤변수 X에 대한 기대값은 식 4와 같습니다.

$$\tag{식 5}E(X) = \exp\left(\mu + \frac{1}{2} \sigma^2\right)$$

위 식 5는 다음과정으로 유도 됩니다(식 6).

\begin{align}\tag{식 6} E(X)&=\int^\infty_{-\infty} xf(x)\, dx \\ &=\int^\infty_0 x \frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)\frac{1}{x}\, dx\end{align}

식 6에서 랜덤변수 X는 로그-노말 분포를 따르므로 범위는 x < 0 이 됩니다. 또한 위 식을 식 7과 같이 치환하여 계산합니다.

\begin{align}\tag{식 7}t&=\frac{\ln(x)-\mu}{\sigma} \Rightarrow x=\exp\left(\sigma t +\mu \right)\\ \frac{dt}{dx}&=\frac{d\left(\frac{1}{\sigma}(\ln(x)-\mu) \right)}{dx} \\&=\frac{1}{\sigma x}\\ dt &=\frac{1}{\sigma x} dx \Rightarrow dx=\sigma x dt=\sigma \exp\left(\sigma t +\mu \right)dt\\ & x \rightarrow 0 \Rightarrow t \rightarrow -\infty \\ & x \rightarrow \infty \Rightarrow t \rightarrow \infty \end{align}

식 7을 식 6에 대입하여 정리하면 식 8과 같습니다.

\begin{align}\tag{식 8} E(X)&= \int^\infty_0 \frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)\\ &=\int^\infty_{\infty} \frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{t^2}{2}\right)\sigma\exp\left(\sigma t +\mu \right)dt \\ \Rightarrow & -\frac{1}{2}t^2+\sigma t+\mu = -\frac{1}{2}(t+\sigma)^2+\left(\frac{\sigma^2}{2}+\mu\right)\,dt\\ & = \frac{1}{\sqrt{2\pi}}\int^\infty_{\infty} \exp\left( -\frac{1}{2}(t+\sigma)^2\right)\exp\left(\frac{\sigma^2}{2}+\mu\right)\, dt\\ &=\exp\left(\frac{\sigma^2}{2}+\mu\right)\int^\infty_{\infty} \frac{1}{\sqrt{2\pi}}\exp\left( -\frac{1}{2}(t+\sigma)^2\right)\, dt\\ \Rightarrow &\text{위 항의 적분은 표준편차 1, 평균이}\, \sigma\,\text{인 정규분포로서 적분 결과는 1입니다.}\\&=\exp\left(\frac{\sigma^2}{2}+\mu\right)\end{align}

분산

로그 노말 분포를 따르는 랜덤변수 X에 대한 분산은 식 9와 같습니다.

$$\tag{식 9}\text{Var}(X) = \exp\left(\frac{2\mu + 2 \sigma^2}{2\mu + \sigma^2}\right)$$

분산은 $E(X^2)-E(x)^2$으로 계산됩니다. 먼저 $ E(X^2)$는 식 10과 같이 결정할 수 있습니다. 이 과정에서 식 7을 치환적분을 실행합니다.

\begin{align}\tag{식 10} E(X^2)&=\int^\infty_{-\infty} x^2f(x)\, dx \\ &=\int^\infty_0 x^2 \frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)\frac{1}{x}\, dx\\&=\frac{1}{\sqrt{2\pi} \sigma} \int^\infty_0 x \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)\, dx\\ &=\exp\left(2\sigma^2+2\mu\right) \end{align}

그러므로 분산은 식 11과 같습니다.

\begin{align}\tag{식 11}\text{Var}(X)&=E(X^2)-E(x)^2\\&= \exp\left(2\sigma^2+2\mu\right) - \left(\exp\left(\frac{\sigma^2}{2}+\mu\right)\right)^2\\&= \exp\left(2\sigma^2+2\mu\right)-\exp 2\left(\frac{\sigma^2}{2}+\mu\right)\\ &= \exp\left(2\sigma^2+2\mu\right)-\exp\left(2\mu+\sigma^2\right)\\& \because\; [\ln(z)]^2 = \ln(2z)\end{align}

높은 차수의 모멘트

n차 모멘트는 식 12와 같이 계산됩니다.

\begin{align}\tag{식 12}E(X^n)&=\int^\infty_{-\infty}x^nF_x(x)\, dx\\ &=\int^\infty_0 x^n \frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)\frac{1}{x}\, dx\\&=\exp \left(\frac{1}{2}n^2\sigma^2+n\mu\right) \end{align}

식 12는 식 7을 적용하여 증명할 수 있습니다.