함수 그래프 그리기: 최대와 최소 찾기

작성된 그림은 전자책 파이썬과 함께하는 미분적분에서 Chapter 5.1에서 소개한 여러 그래프들과 그 코드입니다.

import numpy as np 
from sympy import *
import matplotlib.pyplot as plt
import seaborn as sns

def tgline(slope, x0, y0, x):
    b=y0-slope*x0
    re=slope*x+b
    return(re)
def scantline(x0, y0, x1, y1, x):
    s, b=symbols("s, b")
    eq1=x0*s+b-y0
    eq2=x1*s+b-y1
    re=solve([eq1, eq2], (s, b))
    re1=float(re[s])*x+float(re[b])
    return(re1)

CH 5.1

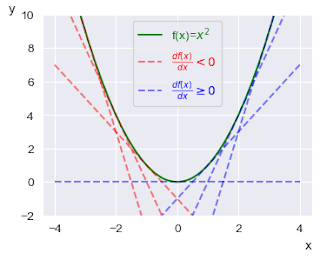
#그림 5.1.1
x=np.linspace(-4,4, 100)
y=x**2
plt.figure(figsize=(4, 3))
plt.plot(x, y, color="g", label=r"f(x)=$x^2$")
for i in np.arange(-3, 4):
    if i==-1:
        nme=r"$\frac{df(x)}{dx} < 0$"
    elif i==1:
        nme=r"$\frac{df(x)}{dx} \geq 0$"
    else:
        nme=""
    plt.plot(x, tgline(2*i, i, i**2, x), ls="--", alpha=0.5, color=['r' if i < 0 else 'b'][0], label=nme)
plt.xlabel("x", loc="right", fontsize="11")
plt.ylabel("y", rotation="horizontal", loc="top", fontsize="11")
plt.ylim([-2, 10])
plt.legend(loc="best", labelcolor=['g','r', 'b'])
plt.show()

#그림 5.1.2
x=np.linspace(-4,4, 100)
y=x**2
plt.figure(figsize=(4, 3))
plt.plot(x, y, color="g", label=r"f(x)=$x^2$")
plt.plot(x, scantline(-1,1, -3, 9, x), ls="--", lw=2, alpha=0.6, color="b")
plt.plot(x, scantline(1,1,3,9, x), ls="--", lw=2, alpha=0.6, color="r")
px, py=[(-3,-1,3, 1), (9, 1, 9, 1)]
nme=['a', 'b', 'c', 'd']
col=['b','b','r','r']
for i in range(4):
    plt.scatter(px[i], py[i],  s=50, c=col[i])
    plt.text(px[i]+0.2, py[i], f"({nme[i]}, f({nme[i]}))", color=col[i])
plt.hlines(0, -4, 4, lw=0.7, color="gray")
plt.vlines(0, -3, 16, lw=0.7, color="gray")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal", fontsize="11")
plt.xticks([])
plt.yticks([])
plt.ylim([-2, 12])
plt.legend(loc=(0.5, 0.8), labelcolor='g', frameon=False)
plt.show()

#그림 5.1.3
a=symbols('a')
f=(a-1)*(a-2)*(a-3)
df=diff(f, a)
sol=solve(df, a)
x=np.linspace(0, 6, 100)
y=[f.subs(a, i) for i in x]
y1=[df.subs(a, i) for i in x]
plt.figure(figsize=(4, 3))
plt.plot(x, y, color="g", label="f(x)=(x-1)(x-2)(x-4)")
plt.plot(x, y1, color="b", label=r"$\frac{df(x)}{dx}=3x^2-12x+11$")
plt.scatter([sol[0], sol[1]], [df.subs(a, sol[0]), df.subs(a, sol[1])], c="r", s=50,label=r"$\frac{df(x)}{dx}=0$")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal", fontsize="11")
plt.ylim([-2, 3])
plt.legend(loc=(0.7, 0.6), labelcolor=['g','b'])
plt.show()

#그림 5.1.4
x=np.linspace(-1, 1, 100)
f=x**2
y=tgline(2*0.3, 0.3, 0.09, x)
y1=tgline(2*(-0.3), -0.3, 0.09, x)
plt.figure(figsize=(4, 3))
plt.plot(x, f, color="g", label=r"f(x)=$x^2$")
plt.plot(x, y1, ls="--", alpha=0.6, color="b")
plt.plot(x, y, ls="--", alpha=0.6, color="r")
plt.scatter(-0.3, 0.09, color="b", s=50,label="A")
plt.scatter(0,0, color="k", s=50,label="B(cv, min)")
plt.scatter(0.3, 0.09, color="r", s=50,label="C")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal", fontsize="11")
plt.ylim([-0.5,0.5])
plt.legend(loc="best", labelcolor=['g','b','k','r'])
plt.show()

#그림 5.1.5
x=np.linspace(-10, 10, 100)
a=symbols("a")
f=a**4-6*a**3-8*a**2+2
df=f.diff(a)
sol=solve(df, a)
y=[f.subs(a, i) for i in x]
y1=[df.subs(a, i) for i in x]
plt.figure(figsize=(4, 3))
plt.plot(x, y, color="g", label="f(x)")
plt.plot(x, y1, color="b", label=r"$\frac{df(x)}{dx}$")
plt.scatter(sol[0], f.subs(a, sol[0]), s=50, c='r', label="A")
plt.scatter(sol[1], f.subs(a, sol[1]), s=50, c='brown', label="B")
plt.scatter(sol[2], f.subs(a, sol[2]), s=50, c='orange', label="C")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal", fontsize="11")
plt.ylim([-400, 400])
plt.legend(loc="best", labelcolor=['g','b','k','r'], frameon=False)
plt.show()

#그림 5.1.6
x=np.linspace(-2, 3, 100)
a=symbols("a")
f=2*a**3-3*a**2-12*a+12
df=f.diff(a)
sol=solve(df, a)
y=[f.subs(a, i) for i in x]
y1=[df.subs(a, i) for i in x]
plt.figure(figsize=(4, 3))
plt.plot(x, y, color="g", label="f(x)")
plt.plot(x, y1, color="b", label=r"$\frac{df(x)}{dx}$")
plt.scatter(sol[0], f.subs(a, sol[0]), s=50, c='r', label="A")
plt.scatter(sol[1], f.subs(a, sol[1]), s=50, c='brown', label="B")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal", fontsize="11")
plt.legend(loc='best', labelcolor=['g','b','k','r'])
plt.show()

#그림 5.1.7
a=symbols('a')
f=2*a**3-a**4
df=f.diff(a)
sol=solve(df, a)
x=np.linspace(-2, 3, 100)
y=[f.subs(a, i) for i in x]
y1=[df.subs(a, i) for i in x]
plt.figure(figsize=(4, 3))
plt.plot(x, y, color="g", label="f(x)")
plt.plot(x, y1, color="b", label=r"$\frac{df(x)}{dx}$")
plt.scatter(sol[0], f.subs(a, sol[0]), s=50, c='r', label="A")
plt.scatter(sol[1], f.subs(a, sol[1]), s=50, c='brown', label="B")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal",fontsize="11")
plt.ylim([-5, 5])
plt.legend(loc="best", labelcolor="linecolor")
plt.show()

#그림 5.1.8
x1=np.linspace(-2, 1.999, 30)
x2=np.linspace(2.001, 10, 70)
y1=np.cbrt((x1-2)**2)+1
y2=np.cbrt((x2-2)**2)+1
plt.figure(figsize=(4, 3))
plt.plot(x1, y1, color="g", label="f(x)")
plt.plot(x2, y2, color="g")
plt.scatter(2, 1, s=50, c='white', edgecolors="k")
plt.xlabel("x", fontsize="11")
plt.ylabel("y", rotation="horizontal",fontsize="11")
plt.legend(loc="best", labelcolor="g")
plt.show()

#그림 5.1.9
t=symbols('t', positive=True)
p=(1-exp(-0.004*t))*1000000*500-1000000*t
dp=p.diff(t)
cp=solve(dp, t)
x=np.linspace(0, 500, 500)
y=[p.subs(t, i) for i in x]
y1=[dp.subs(t, i) for i in x]
f, ax=plt.subplots(1,1, figsize=(4,3))
plt.plot(x, y, color="g")
plt.scatter(cp[0], p.subs(t, cp[0]), s=30, c="r", label="Maximum")
plt.xlabel("t")
plt.ylabel("p(t)", rotation="horizontal", color="g")
plt.legend(loc="best")
ax2=ax.twinx()
plt.plot(x, y1, ls="dashed", color="b", label=r"$\frac{dp(t)}{dt}$")
plt.ylabel(r"$\frac{dp(t)}{dt}$", rotation="horizontal", color="b")
plt.show()

[Linear Algebra] 유사변환(Similarity transformation)

유사변환(Similarity transformation) n×n 차원의 정방 행렬 A, B 그리고 가역 행렬 P 사이에 식 1의 관계가 성립하면 행렬 A와 B는 유사행렬(similarity matrix)이 되며 행렬 A를 가역행렬 P와 B로 분해하는 것을 유사 변환(similarity transformation) 이라고 합니다.

\begin{matrix} (1) & A = P B P^{- 1} \Leftrightarrow P^{- 1} A P = B \end{matrix}

식 2는 식 1의 양변에 B의 고유값을 고려한 것입니다.

\begin{aligned} (식 2) & B - λ I & = P^{- 1} A P - λ P^{- 1} P \\ = P^{- 1} (A P - λ P) \\ = P^{- 1} (A - λ I) P \end{aligned}

식 2의 행렬식은 식 3과 같이 정리됩니다.

\begin{aligned} \begin{aligned} det (B - λ I) & = det (P^{- 1} (A P - λ P)) \\ = det (P^{- 1}) det ((A - λ I)) det (P) \\ = det (P^{- 1}) det (P) det ((A - λ I)) \\ = det (A - λ I) \end{aligned} \\ \begin{aligned} ∵ det (P^{- 1}) det (P) & = det (P^{- 1} P) \\ = det (I) \end{aligned} \end{aligned}

유사행렬의 특성 유사행렬인 두 정방행렬 A와 B는 'A ~ B' 와 같...

[sympy] Sympy객체의 표현을 위한 함수들

Sympy객체의 표현을 위한 함수들 General simplify(x): 식 x(sympy 객체)를 간단히 정리 합니다. import numpy as np from sympy import * x=symbols("x") a=sin(x)**2+cos(x)**2 a

\sin^{2} (x) + \cos^{2} (x)

simplify(a) 1 simplify(b)

\frac{x^{3} + x^{2} - x - 1}{x^{2} + 2 x + 1}

simplify(b) x - 1 c=gamma(x)/gamma(x-2) c

\frac{Γ (x)}{Γ (x - 2)}

simplify(c)

(x - 2) (x - 1)

위의 예들 중 객체 c의 감마함수(gamma(x))는 확률분포 등 여러 부분에서 사용되는 표현식으로 다음과 같이 정의 됩니다. 감마함수는 음이 아닌 정수를 제외한 모든 수에서 정의됩니다. 식 1과 같이 자연수에서 감마함수는 factorial(!), 부동소수(양의 실수)인 경우 적분을 적용하여 계산합니다.

\begin{matrix} (식 1) & Γ (n) = {\begin{cases} (n - 1)! & n : 자연수 \\ \int_{0}^{\infty} x^{n - 1} e^{- x} d x & n : 부동소수 \end{cases} \end{matrix}

x=symbols('x') gamma(x).subs(x,4)

6

factorial 계산은 math.factorial() 함수를 사용할 수 있습니다. import math math.factorial(3) 6 a=gamma(x).subs(x,4.5) a.evalf(3) 11.6 simpilfy() 함수의 알고리즘은 식에서 공통사항을 찾아 정리하...

sympy.solvers로 방정식해 구하기 대수 방정식을 해를 계산하기 위해 다음 함수를 사용합니다. sympy.solvers.solve(f, *symbols, **flags) f=0, 즉 동차방정식에 대해 지정한 변수의 해를 계산 f : 식 또는 함수 symbols: 식의 해를 계산하기 위한 변수, 변수가 하나인 경우는 생략가능(자동으로 인식) flags: 계산 또는 결과의 방식을 지정하기 위한 인수들 dict=True: {x:3, y:1}같이 사전형식, 기본값 = False set=True :{(x,3),(y,1)}같이 집합형식, 기본값 = False ratioal=True : 실수를 유리수로 반환, 기본값 = False positive=True: 해들 중에 양수만을 반환, 기본값 = False 예

x^{2} = 1

의 해를 결정합니다. solve() 함수에 적용하기 위해서는 다음과 같이 식의 한쪽이 0이 되는 형태인 동차식으로 구성되어야 합니다.

x^{2} - 1 = 0

import numpy as np from sympy import * x = symbols('x') solve(x**2-1, x) [-1, 1] 위 식은 계산 과정은 다음과 같습니다.

\begin{array}{r} x^{2} - 1 = 0 \to (x + 1) (x - 1) = 0 \\ x = 1 or - 1 \end{array}

예

x^{4} = 1

의 해를 결정합니다. solve() 함수의 인수 set=True를 지정하였으므로 결과는 집합(set)형으로 반환됩니다. eq=x**4-1 solve(eq, set=True) ([x], {(-1,), (-I,), (1,), (I,)}) 위의 경우 I는 복소수입니다.즉 위 결과의 과정은 다음과 같습니다.

x^{4} - 1 = (x^{2} + 1) (x + 1) (x - 1) = 0 \to x = \pm \sqrt{- 1}, \pm 1 = \pm i, \pm 1

실수...

sons dataStory

이 블로그 검색

[matplotlib] 등고선(Contour)