[stock] 이동평균선에 대해

이동평균선

첫번째 역할은 가격 변동을 매끄럽게 표현하는 것입니다. 예를 들어 20일 이동평균은 20일 동안의 평균값의 추이를 나타냄. 20일 평균과 당일 가격 비교

• 20일 이동평균 < 당일 가격: 과거 20일 사이에 매수한 트레이더가 이익을 봤음을 의미(공매도인 경우는 손해)
• 20일 이동평균 > 당일 가격: 과거 20일 사이에 매수한 트레이더가 손해를 봤음을 의미(공매도인 경우는 이익)

이동평균의 추이를 관찰하는 것으로 시간의 경과에 따라 이익 또는 손실의 확대 또는 축소를 관찰 할 수 있다. 매수 포지션을 가진 쪽이 이익을 봤고 유리한 경향이 지속할 것 같다면 추격매수를 검토할 것이다. 이런 국면이면 매도 포지션을 가진 쪽이 손절을 위한 매수를 검토함으로써 가격이 더욱 상승할 지 모른다. 또는 매수포지션을 가진 쪽이 이익 실현을 위해 매도를 생각할지 모른다. 즉, 평균 매수가(또는 평균 매도가)를 파악하고 그것을 현재의 가격과 비교해서 시장에 참가한 트레이더들의 현재 손익 상황이 어떠한지를 분석하면 앞으로 어떤 흐름이 될 가능성을 추리할 수 있다.

골든크로스, 데드크로스

이동평균선을 기준으로 현재 가격의 위치에 따라 향후 가격 변동향에 큰 의미를 지닌다. 그래서 이동평균선에서 현 가격의 위치 변화 지점을 "크로스포인트(교차점)"이라 합니다.

• 골든크로스: 현 가격이 이동평균선 아래에서 위로 상승하는 지점
  대전제는 이동 평균선이 한동안 하락하고 있고 그 이동 평균선이 하락을 멈출적으로 예상되는 조짐이 존재에서 단기선이 장시건을 아래에서 위로 교차하여 지나가는 것
• 데드크로스 : 현 가격이 이동평균선 위에서 아래로 하락하는 지점
  이동평균선이 횡보 상태이거나 약간 하락 기조로 전환의 전제가 필요
  대전제는 이동평균선이 한동안 상승, 그 이동 평균선이 상승을 멈출것으로 예상되는 조짐이 있을 것

import numpy as np 
import pandas as pd 
import yfinance as yf
import matplotlib.pyplot as plt

st=pd.Timestamp(2024, 1,20)
et=pd.Timestamp(2024, 9,24)
d=yf.download("005930.KS", start=st, end=et)
ma20=d.Close.rolling(20).mean().dropna()
plt.figure(figsize=(6,3))
plt.plot(d.index, d.Close, color="b")
plt.plot(d.index[19:], ma20, color="r")
plt.show()

크로스 발생에서의 심리변화

골든 크로스	전	손익이 마이너스 상태이므로 언제 손절할 지 고민
	후	손익이 플러스 전환되었으므로 추격매수를 검토
데드크로스	전	손익이 플러스 상태이므로 안심하고 포지션 보유
	후	손익이 마이너스로 전환되었으므로 당황하며 손절 검토

위 표와 같은 이유로 일반적으로 골든크로스는 매수신호, 데드크로스는 매도신호가 됩니다. 그러나 이와 같이 단순히 접근하기에는 오신호 발생으로 위험하다. 즉, 매수신호후 하락세 전환, 매두신호 신호후 상승세 전환이 일어날 수 있다. 이러한 이유로 이동 평균선과 실제 가격의 관계를 조금 더 세밀하게 파악할 필요가 있습니다. "그랜빌의 법칙"을 참조할 수 있다.

• 매수 신호
  • 이동 평균선이 어느정도의 기간 동안 하락한 위 횡보하거나 약간의 상승 기조로 전환된 시기에 가격이 그 이동평균선을 아래에서 위로 뚜렷하게 교차했을 때
  • 이동 평균선이 지속적으로 상승하는 시기에 가격이 이동평균선을 일시적으로 밑돌았을 때
  • 가격이 상승 기조의 이동평균선보다 위에 있고 그 후 이동 평균선을 향해 접근(하락)하지만 이동 평균선과 교차하지 않고 다시 상승하기 시작했을 때
  • 가격이 하락 기조의 이동평균선보다 아래에 있고 이동평균선으로부터 크게 괴리되었을 때
    이동평균 괴리율로 표시
    • $\text{이동 평균 괴리율}=\frac{\text{당일의 종가}-\text{이동 평균값}}{\text{이동 평균값}}$
    • 이동평균과의 괴리된 가격은 다시 이동평균으로 회귀하는 특성을 이용하는 것이지만 신호가 되는 괴리율 수치는 일정하지 않기 때문에 실제 적용에 유의해야 함. 사용하기 까다로운 규칙은 단지 참고 정도로 고려해야한다.
• 매도 신호
  • 이동 평균선이 어느정도의 기간동안 상승한 위 횡보하거나 약간 하락 기조로 전환된 시기에 가격이 그 이동 평균선을 위에서 아래로 뚜렷하게 교차
  • 이동 평균선이 지속적으로 하락하는 시기에 가격이 이동 평균선을 일시적으로 웃돌았을 때
  • 가격이 하락 기조의 이동 평균성보다 아래에 있고 그 후 이동 평균선을 향해 접근하지만 교차 없이 다시 하락할 경우
  • 가격이 상승 기조의 이동 평균선보다 위에 있고 이동 평균선으로부터 크게 괴리 되었을 때

두 개의 이동평균선(단기선, 중기선)

가격과 이평선이 아닌 두개의 이평선의 사용은 오신호를 줄이기 위해서 사용합니다. 단기선(5일)과 20일 이평선(중기)에 골든, 데드 크로스 적용

5와 20일 이평선을 적용할 경우 기준이 되는 것은 20일 선. 즉 최근 20일 사이에 매수(매도) 포지션이 현재(과거 5일의 평균적 상황) 어떤 상황인지를 살펴본다. 그들의 손익이 평균적으로

• + 또는 -?
• +와 - 를 오가는가?
• -라면 그 마이너스가 증가하는가 아니면 감소하고 있는가?

골든 크로서란 매수 포지션을 가진 사람들의 평균적인 수익이 그 전까지 마이너스였다가 플러스로 전환되는 포인트, 매도포지션인 사람들의 경우는 플러스였다가 마이너스로 전횐되는 포인트롯 그 포인트에서 매도 세력과 매수 세력의 힘의 관계가 크게 변화한다. 데드크로스일 경우는 반대

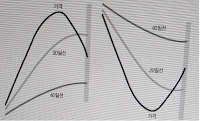
두 개의 이동평균선(중기선, 장기선)

예로 20일선과 40일 선을 조합해서 사용할 경우 '이동 평균선의 대순환 분석'의 기반이 됩니다.

• 위 왼쪽 그림은 과거 40일 동안의 큰 흐름이 상승 추세를 의미, 최근 20일 선은 가격 위에 있으므로 하락 추세임을 나타냅니다. 즉, 상승추세가 최근 하락으로 전환됨을 의미합니다.
• 오른쪽 그림은 장기선(40일선)이 가격의 위에 있는 것으로 과거 40 일 동안의 흐름이 하락 추세 그러나 최근 20일 선이 가격선 아래에 위치하면서 상승으로 전환됨을 의미

이평선의 위치 관계를 보는 것만으로 그 날에 이르기까지 과거의 흐름과 그 날의 상황을 알 수 있습니다. 그리고 이 사실은 이평선 대순환 분석에 중요 포인트가 됩니다.

이평선 대순환 분석으로 에지 발견

트레이딩을 통해 수익을 내기 위해서는 미래를 예측하는 것이 아니라 '현재의 가격 상황이 어떠한가?'를 파악하고 에지가 있는 방향으로 포지션을 갖는 것이 중요

세개의 이평선을 사용하여 가격의 움직임이 어떤 국면에 있는지 명확히 정의하고 상승과 하락의 힘관계를 분석

세개의 이평선의 배열 순서는 총 6가지로 순열을 사용하여 계산할 수 있습니다.

import itertools
x=['단기','중기','장기']
list(itertools.permutations(x, 3))

[('단기', '중기', '장기'),
 ('단기', '장기', '중기'),
 ('중기', '단기', '장기'),
 ('중기', '장기', '단기'),
 ('장기', '단기', '중기'),
 ('장기', '중기', '단기')]

위 결과와 같이 각 배열 순서에는 논리적인 근ㄴ거에 입각한 의미(가격 상황)이 존재하며 각 단계에서 다음 단계로 이동할지, 이동한다면 어떤 단계로 갈지로 추정할 수 있습니다. 이와 같은 이평선 대순환 분석을 활용하면 다음 행동을 계획할 수 있습니다.

위 이평선의 배열은 다음과 같이 각 단계로 순서대로 이어진다는 것이 이평선 대순환 분석의 기본 발상입니다. 각각의 단계는 현재의 가격 상황을 나타내는 메시지가 있습니다.

단계	배열
1단계	'단기', '중기', '장기'	안정상승
2단계	'중기', '단기', '장기'	상승추세의 끝
3단계	'중기', '장기', '단기'	하락추세의 시작
4단계	'장기', '중기', '단기'	안정하락
5단계	'장기', '단기', '중기'	하락 추세의 끝
6단계	'단기', '장기', '중기'	상승 추세 시작

위 그림은 일반적으로 이루어지는 대순환을 나타내는 것으로 당연히 예외도 존재합니다. 즉, 위의 1단계에서 6단계로 진행하는 역행이 일어나기는 하지만 위 과정보다는 일반적이지 않습니다.

역행의 경우 눌림목이나 일시적으로 반등 혹은 박스 국면에 있는 경우입니다. 또한 역행은 오래 지속되지 않는 특성이 있습니다. 그러므로 역행이 일어나는 경우 순행으로 회귀한다는 것을 염두에 두어야 합니다.

역행이든 순행이든 단계를 건너뛰는 경우는 일어나지 않습니다. 그러므로 현재 단계와 순행 또는 역행을 결정할 수 있으면 다음 단계가 명확해 짐을 의미합니다.

• 1단계와 4단계는 기본적으로 오래 지속
• 2단계 ~ 3단계, 5단계 ~ 6단계는 이행기(변화기)이므로 기본적으로 빠르게 지나감
• 1,4 단계가 짧고 2,3,5 그리고 6 단계가 길 때는 박스권 상태일 가능성이 높음

현 단계와 추이 파악이 되며 위 각 단계의 특성을 이해 할 수 있음. 그러므로 현 단계와 추세 파악이 중요

• 1 단계 → 2단계: [5일선, 20일선, 40일선] → [20일선, 5일선(데드크로스 발생), 40일선]
  매수포지션을 가진 쪽의 과거 1개월의 수익이 + → - 전환을 의미
• 2단계 → 3단계: 단기선이 장기선 아래로 내려감(두 선사이에 데드크로스)

이평선 대순환 분석에서는 단기선, 중기선, 장기선이라는 세 이평선의 배열순서, 가격, 기울기에 주목하고 이 세가지 요소를 바탕으로 분석을 실시

• 1단계
  • 가격 상승→ 단기선 상승→ 중기선 상승 →장기선 상승
  • 세 이평선이 모두 우상향 매수에 에지가 있는 상태, 즉 명확한 상승추세(세 이평선이 정배열이지만 모두 우상향이 아니라면 1단계가 끝나고 박스구간 돌입의 가능성이 있음)
  • 세 이평선의 간격이 계속 별어지는 상태라면 더욱 공격적 매수

2단계에서 가격이 하락 추세로 전환될 때는 움직임이 빠른 단기선이 제일 먼저 하락으로 전환되어 중기선을 위에서 아래로 교차로 이평선은 중기, 단기 , 장기의 순서가 됩니다. 다만 일시적 눌림목이 형성되는 경우도 있습니다. 이 경우는 1단계로 돌아갑니다. 그러므로 1단계에서 신규로 취했던 매수포지션을 청산할 타이밍이지만 이평선을 교차에서 중기선과 장시건이 안정 상승을 지속하고 있다면 포지션 유지. 즉, 중기선과 장기선이 형성하는 띠가 우상향이고 넓은 간격을 유지하고 있는 한은 단기선이 조금 하락했더라도 추세가 강하다고 판단합니다.

원칙적으로 2단계는 하락추세로 접어드는 첫 조짐이므로 매도를 고려(일부만).

1단계의 상승이 단기간에 끝나 버렸을 경우 박스 장세로 접어들 가능성이 있습니다. 이것을 파악하기 전 까지는 매도 포지션을 취하지 않는다. 단기선이 계속 하락하고 있을것, 중기선의 상승이 끝나고 거의 평행해졌을 때가 매도 포지션을 취하기 위한 조건입니다.

단기선이 중기와 장기 사이에 위치할 경우 어느선과 교차가 포인트가 됩니다. 일반적으로 장기선과 교차하여 3단계로 진행하는데 중기선과 교차로 1단계로 회귀하는 경우도 발생(상승장의 눌림목이었을 때 자주 볼 수 있는 전개). 이것을 예측하기 위한 힡느는 장기성의 기울기입니다. 장기선의 상승에 변화가 보이지 않을 경우는 장기선과 교차하지않거나 교차하더라도 곹 오신호가 될 가능성이 크다고 말할 수 있습니다.

3단계에서

2단계에서 하락경향이 더욱 계속되면 단기선은 장기선 아래로 내려가면서 중기, 장기, 단기선의 순서로 배열 즉, 하락장의 시작입니다. 1단계에서 매수 포지션을 모두 청산. 이 경우 다음 조건을 확인

• 1 단계가 길었을 것
• 1, 2, 3단계의 순서로 진행되었을 것
• 단기선과 중기선이 우하향이고 장기선도 평행상태에 가까울 것

위 조건의 충족 상태에서 신규로 매도 포지션을 취한 뒤에도 단기선이 상승해 다른 선과 교차 했다면 즉시 청산을 고려. 중기선과 장기선이 교차하여 장기, 중기선의 순서가 되면 안정하라기에 접어드는 것이 일반적 그러나 단기선이 일찍 상승하면서 다시 장기선과 고차해 2단계로 돌아가는 경우가 있습니다. 이 경우는 발스 장세에 돌입가능성이 증가 3단계이후 움직임 파악의 중요 포인트는 장기선의 움직임으로 4단계 안정하락기로 이행하기 위해서는 장기선의 상승이 끝나야 한다.

4 단계에서

장기, 중기, 단기선의 배열로 모두 우하향입니다(세 이평선이 모두 우하향이 아니라면 이 단계가 짧은 기간에 끝나고 박스 장세에 돌입할 가능성이 있다). 특히 세 이평선의 간격이 계속 벌어지는 상태라면 4단계의 진행이 굳어짐. 또한 일반적으로 상승추세보다 하락 추세의속도가 더 빠른 경향이 있다.

5 단계에서

가격이 상승 추세로 전환될 때는 단기선이 제일 먼저 상승 전환되어 장기, 단기, 중기의 순서가 된다. 다만 일시적 반등 가능성을 고려해야 한다. 이 경우 4 단계로 회귀. 그러므로 5단계는 매도 포지션 청산 시기이지만 이평선의 교차에소 중기과 장기의 하락이 지속되는 경우, 이들이 형성하는 띠가 우하향이고 넓은 간격을 위지하는 한 단기선이 조금 상승했더라도 하락 추세가 강하다고 판단

원칙적으로 상승추세에 접어드는 첫 조짐이므로 매수의 일부만을 실행 또한 4 단계의 하락이 단기간에 끝아 버렸을 경우 박스장에 돌입할 가능성을 고려. 그러므로 매수 포지션을 취하지 않는다.

단기선이 계속 상승, 중기선의 하락이 끝나고 거의 ㅍㅇ향해졌을 때가 매수 포지션을 취하기 위한 조건이 된다.

이 단계에서는 단기선이 장기와 중기 사이에 배열되는데 어느선과의 교차가 중요해 진다. 일반적으로 단기선이 장기선과 교차해 6단계로 이행하지만 아래의 중기선과 교차하면 4단계로 회귀하게 된다(하락장의 일시적 반등이었을 때 자주 볼 수 있는 전개).이것은 장기선의 기울기로 판단할 수 있다. 장기선의 하락에 변화가 보이지 않을 경우는 장기선과 교차하지 않거나 교차하더라도 곹 오신호가 돌 가능성이 크다고 할 수 있다.

6 단계에서

5 단계에서 상승추세가 계속되면 단기선은 장기선위로 올라가며 단기, 장기, 중시의 배열이 된다. 즉, 상승장의 시작이다. 여기에서 매도 포지션이 있을 경우 전부 청산한다. 또한 매수 포지션의 조기 주문을 검토. 그러나 오신호의 가능성을 함께 고려하여 매수는 일부만 진행한다. 조기주문 실행에 다음 조건 충족여보를 확인

• 4단계의 기간이 길었을 것
• 4단계, 5, 6 단계의 순서로 이행
• 단기선과 중기선이 우상향이고 장기선도 평형상태에 가까울 것

매수 포지션을 취한 후 단기선이 하강해 다른 선과 교차했다면 즉시 청산 단기선이 하락하여 장시건과 교차해 5단계로 돌아가는 경우가 있다. 이 경우 박스장에 돌입할 가능성이 커짐. 안정상승기로 이행을 위해서는 장기선의 하락이 끝나야 한다.