내용
본 글은 한국은행의 "알기 쉬운 경제이야기" 일곱째 마당의 모든 내용을 블로그 형식으로 다시 작성한 것입니다.
국민소득과 경제성장
한 나라의 경제성적표, '국민소득'이란?
국민소득 통계, 20세기 최고의 발명품 중 하나
어떤사람의 경제적 지위를 알고 싶을 때 우리는 그 사람의 소득 수준을 알아봅니다. 소득이 많은 사람은 적은 사람에 비해 상대적으로 더 많은 상품이나 서비스를 구입하고, 좋은 주택과 고급 자동차를 소유햘 수 있는 등 더 나은 생활을 할 수 있습니다. 이와 마찬가지로 국가경제도 얼마나 풍요로운지 판단하려면, 그 나라의 각 경제주체의 소득을 합한 국민소득을 살펴봅니다. 한 나라의 경제상황을 나타내는 경제지표에는 여러 가지가 있습니다. 예를 들어 철도 운송량과 철강 생산량, 경상지수, 외환보유액 등 개별 경제지표가 과거에 비해 열마나 늘어났는지 또는 다른 나라와 비교하여 어느 정도의 수준에 이르는지를 가지고 판단할 수 있습니다. 그러나 이러한 지표들은 국민경제의 한 면만을 나타낼 뿐이며 나라 전체의 종합적인 경제상황을 보여준다고 하기 어렵습니다. 가령 우리나라의 외환보유액이 독일보다 많다고 해서 우리나라가 독일 보다 경제수준이 높다고 판단하거나, 대만의 경상수지가 흑자라고 해서 경상수지 적자국인 미국보다 경제수준이 높다고 말할 수는 없는 것입니다.
이에 따라 세계 각국은 국민경제의 활동수준을 종합적으로 판단하기 위해 국민소득이란 경제지표를 만들어 사용하고 있습니다.
국민소득은 어떻게 측정하나?
어떤 기업의 자산이나 부채가 어느 정도이며 손익이 얼마인지는 그 기업의 재무상표나 손익계산서 등의 재무제표를 보면 알 수 있습니다. 이러한 재무제표는 일정한 기준에 따라 만들어지기 떄문에 작성자의 정직성을 담보로 이를 신뢰하고 있습니다. 이와 마찬가지로 한 나라 경제의 종합적인 성적표라 할 수 있는 국민소득 통계도 국제적으로 통일된 기준에 의해 작성되고 있습니다. 현재 우리나라의 국민소득 통계는 유엔 등이 각국에 권고한 국제기준인 '2008년판 국민계정체제(SNA:System of Nationala Accounts 2008)'에 따라 한국은행에 의해 작성되고 있습니다. 그리고 국민소득 통계는 경제구조의 변화 등을 반영하기 위해 기준연도를 5년 단위로 변경하고 있는데 2019년에 기준연도를 2015년으로 개편한 바 있습니다. 이러한 국민소득은 어떻게 측정할까요? 가장 흔히 사용하는 방법은 각 경제 주체들이 창출한 생산물의 가치를 더하여 구하는 것입니다. 이것이 바로 일반 사람들이 널리 알고 있는 국내총생산(GDP: Gross Domestic Procduct)이라는 것입니다.
통상 1년 동안에 한 나라의 영토 안에서 생산되어 최종적인 용도로 사용되는 재화와 서비스의 가치를 모두 합한 것
그린스펀(Alan Greenspan) 전 연궂의장은 1999년 12월 당시 데일리(Willian M. Daley) 상무장관과 베일리(Martin Bailey) 백악관 경제자문위원회 의장과 함께 국내총생산(GDP) 통계를 편제하는 일을 미국 상무부의 20세기 최대 업적으로 평가한 바 있습니다.
국내총생산 통계는 1930년대 초 경제학자 쿠즈네츠(Simon Kuznets)에 의해 개발되었습니다. 이 공로로 쿠즈네츠는 1971년 노벨경제학상을 받았습니다. 이 통계가 개발되기 전이었던 대공황 시기에 미국의 루스벨트(Franklin D. Roosevelt) 대통령과 정책입안자들은 철도 운송량, 철강 생산량 등과 같은 개별 경제지표를 파악하고 있었지만 전체 경제상황을 알기 어려웠습니다. 그러나 국내총생산 통계를 사용한 이후에는 이 통계가 종합적인 경제상황에 대해 유용한 정보를 제공함에 따라 경제를 분석하고 정책을 결정하기 쉬워졌습니다.
국내총생산이란 '일정기간 동안 한 나라 안에서 새로 생산한 재화와 서비스의 가치를 시장가격으로 평가하여 모두 더한 것'입니다. 국내총생산의 의미를 보다 정확하게 ㅇ해하기 위해서는 이 개념을 몇 구절로 나누어 살펴보면 됩니다. 우선 '일정기간 동안'이란 통상 1년을 말합니다. 어떤 한 해의 국내총생산에는 그 해에 새로 생산된 상품으 가치만이 포함되며 그 이전에 만들어져 존재하는 상품의 가치는 포함되지 않습니다. 다음으로 '한 나라 안에서'라는 표현은 생산의 주체가 누구인지와 관계없이 한 나라 국경안에서 생산된 재화와 서비스의 가치를 모두 국내 총생산에 포함시킨다는 것을 뜻합니다. 예를 들어 우리나라에서 기업활동을 하고 있는 A국 기업에 의해 생산된 상품의 가치도 우리나라의 국내총생산에 포함됩니다. 반면에 A국에서 활동하고 있는 한국 기업에 의해 생산된 상품의 가치는 A국 국내총생산에 포함됩니다.
마지막으로 '새로 생산한 재화와 서비스의 가치'란 각 생산단계에서 추가된 가치, 즉 부가가치를 말합니다. 최종 생산된 상품의 가치를 모두 합하면 그 상품을 만드는 데 원재료로 사용된 중간투입물의 가치가 중복 계산됩니다. 따라서 새로 생산한 부가가치를 계산하기 위해서는 상품을 생산하는 데 사용되는 중간투입물의 가치를 제외시켜야 합니다. 예를 들어 어떤 공장에서 철강, 가죽, 유리 등 원재료 비용을 1000만 원 들여 2000만 원짜리 승용차 1대를 만들었다고 가정해 봅시다. 그러면 이 공장의 산출액은 2000만 원, 중간투입액은 1000만 원이므로 이 공장에서 새로 생산한 가치는 산출액(2000만 원)에서 중간투입액(1000만 원)을 제외한 1000만 원이 됩니다. 그러나 자동차의 원재료로 사용된 철강, 가죽, 유리 등도 어떤 원재료를 투입하여 만들어 낸 것이므로 그것을 만들 때 새로 생산한 가치가 있을 것입니다. 이렇게 각 단계에서 추가로 창출된 가치를 합산하면 결국 최종적인 용도로 사용되는 재화와 서비스의 가치와 같게 됩니다. 즉 위의 단순한 예에서 국내총생산은 최종재인 승용차의 가치인 2000만 원 입니다.
국내총생산과 함께 국민소들의 개념으로 국민총소득(GNI: Gross National Income)이라는 것이 널리 쓰이고 있습니다. 국내총생산은 한 나라의 '영토'안에서 생산한 최종재의 가치를 뜻하는 데 비해 국민총소득은 그 나라 '국민'이 벌어들인 소득의 합계를 나타낸다는 데 차이가 있습니다. 즉, 국내총생산은 나라 안에서 생산된 것이라면 생산의 주체가 누구든 관계없이 모두 포함시켜 계산합니다. 반면에 국민총소득은 누구의 소득인지, 즉 생산주체의 국적을 기준으로 하여 계산합니다. 이렇게 국내와 국민으로 구분하는 이유는 국가 간에 자본과 노동 등 생산요소의 이동이 활발해진 데 있습니다. 이에 따라 흔히 두 지표는 목적이 다소 다르게 이용됩니다. 오늘날 한 나라의 종합적인 경제활동 상황을 파악하고자 할 때에는 국내 개념이 더 중시되고 있습니다. 세계화의 진전으로 외국에 진출하여 현지인을 고용하는 다국적기업의 수가 급격히 늘어나면서 이들 기업이 실제 영업하고 있는 국가의 고용과 경기 등에 영향을 크게 미치기 때문입니다. 그러나 한 나라 국민의 생활 수준을 파악하고자 할 때에는 경제주체가 외국에서 벌어들인 소득도 감안하는 국민총소득을 많이 사용하고 있습니다.
통상 1년 동안에 한 나라 국민이 벌어들인 소득을 합한것
국민소득에서 3면 등가란?
앞에서 국내총생산과 국민총소득의 두 가지 용어를 간략하게 살표보았습니다. 두 용어에서 국냉와 국민을 빼면 총생산과 총소득이 남습니다. 이는 생산과 소득이라고 각각 달리 표현하였지만 사실은 같은 것입니다. 한 나라의 경제는 가계, 기업, 정부 등 각 경제주체들이 재화와 서비스를 생산하고 생산활동에 참여한 대가로 소득을 얻어 그 소득을 다시 재화나 서비스를 구입하기 위해 지출하는 등의 과정을 끊임없이 반복하고 있습니다.
기업은 근로자를 고용하고 돈과 토지를 빌려 생산활동을 함으로써 새로운 부가가치를 창출합니다. 이렇게 생산된 부가가치의 합계를 총생산, 즉 '생산국민소득'이라 합니다. 이 부가가치는 생산활동에 참여한 근로자의 임금, 기업의 이윤 등으로 이루어 집니다. 이러한 생산요소 투입의 대가로 받는 임금·이자·임대료·이윤을 모두 합하여 '분배국민소득'이라 말합니다. 이렇게 분배된 소득은 물건을 구입하여 소비하는 데 쓰이기도 하고, 조세로 납부되어 정부가 여러가지 재정 활동을 하는 데 사용되기도 합니다. 그리고 그 나머지는 저축되어 기업이 건물을 짓거나 생산시설을 갖추는 등의 투자행위에 사용되기도 합니다. 이처럼 소득은 가계와 정부의 소비지출, 기업의 투자지출 등으로 모두 지출되는데 이를 '지출국민소득'이라 합니다. 이러한 국민소득의 세 가지 측면인 생산, 분배, 지출은 그 크기가 같기 때문에 이를 '국민소득 3면 등가의 법칙'이라 합니다.
국민소득의 세 가지 얼굴인 만들어서(생산), 나누어 갖고(분배), 쓰는(지출) 양이 크기가 모두 같은 것
이처럼 국민소득 통계는 세가지 면에서 파악할 수 있는데 보통은 생산지표와 소득지표의 두 가지를 많이 사용하고 있습니다. 과거에는 국내총생산과 같은 생산지표를 주로 사용하였지만 최근 들어 국내총소득(GDI), 국민총소득(GNI)과 같은 수득지표의 사용이 늘고 있는 추세입니다. 유엔 등이 각국의 구매력 수준을 비교하면서 소득지표의 사용을 권고하고 있기 때문입니다. 따라서 이 책에서는 국민소득을 그동안 익숙하게 사용하여 온 생산지표를 중심으로 설명하되 새로운 소득지표가 더 적합한 경우에는 그것을 이용하도록 하겠습니다.
명목국민소득과 실질국민소득
국민소들은 계산할 때 적용하는 시장가격이 당해연도 가격인지, 특정연도(기준연도) 가격인지에 따라 명목국민소득과 실질국민소득으로 나누어 파악하고 있습니다. 명목국민소득은 생산물 수량이 늘어나는 경우뿐만 아니라 가격이 오를 경우에도 커지게 됩니다. 그러나 특정연도의 가격으로 평가하는 실질국민소득은 가격을 고정시켜 놓았으므로 생산량이 늘어나는 경우에만 커집니다. 가령 실질국민소득이 전혀 변동하지 않고 물가가 100% 오른 경우라도 명목국민소득은 2배로 늘어납니다.
이와 같이 국민소득을 명목과 실질로 구분하는 이유는 각각의 쓰임새가 다르기 때문입니다. 일반적으로 명목국민소득은 전체 경제규모, 1인당 국민소득, 경제구조 등을 알아보는 데 주로 이용됩니다. 반면 실질국민소득은 경제성장률을 계산하거나 국민경제가 장기적으로 어떻게 변화하고 있는가를 알아볼 때 주로 이용됩니다.
농부가 자신의 노동력만으로 사과를 생산하여 생산량이 2015년 10만개에서 2019년 12만개로 늘었고 1개당 가격은 2015년 400원에서 2019년 500원으로 올랐다고 가정해 봅시다.
명목소득은 생산량에 당해연도의 가격을 곱하여 계산합니다. 이 경우에 2015년은 사과 10만 개당 가격 400원을 곱한 4000만 원, 2018년은 사과 12만 개 1개 당 가격 500원을 곱한 6000만원이 됩니다. 따라서 농부의 명목소득은 지만 4년 동안 50% 증가하였습니다.
한편 실질소득은 생산량에 기준연도(여기서는 2015년)의 가격을 적용하여 계산합니다. 즉 2015년에는 사과 10만 개에 400원을 곱한 4000만 원, 2019년에는 사과 12만 개에 2015년의 가격인 400원ㅇ르 곱한 4800만 원이 됩니다. 이 경우 농부의 실질 소득은 20% 증가에 그쳤습니다. 이는 실질소득의 증가가 오로지 생산량의 변화에 의해서만 이루어지고 가격 상승의 영향을 받지 않기 때문입니다.
유엔의 국민계정체계는 한 나라의 국민소득을 생산지표와 소득지표로 구분하도록 권고하고 있습니다. 앞에서 살펴본것처럼 국내총생산(GDP)이란 생산활동을 기준으로 측정한 것으로서 '한 나라의 국민과 외국인이 국내에서 생산한 최종생산물의 가치'입니다. 반면 국내총소득(GDI)은 생산활동을 통하여 벌어들인 소득의 구매력을 나타낸 것입니다. 두 지표는 당해연도 가격으로 평가할 때에는 국민소득 3면 등가의 법칙에 따라 서로 같을 수 밖에 없습니다.
그러나 기준년 가격으로 평가할 때에는 실질 GDP에 교역조건 변화에 따른 실질 무역소익을 합하여 실질 GDI를 구합니다. 양 지표는 비슷한 것 같지만 실제 크기는 다소 차이가 납니다. 예를 들어 우리나라의 2018년 실질 GDP는 1807조 7359억 원인데 비해 실질 GDI는 1811조 87억 원입니다. 이처럼 실질지표에 있어서 두 지표가 서로 다른 것은 수출품과 수입품의 가격 사이의 상대적 비율, 즉 교역조건에 변화가 오면 그 나라 국민의 실질 구매력에도 변화가 있기 때문입니다.
간단한 예를 들어 설명해 보겠습니다. 어떤 나라가 전년에 반도체를 20만 개 생산해 1개당 4달러에 전량 수출하고 배럴당 100달러의 가격으로 원유 8천 배럴을 수입하였는데, 금년 들어 반도체 수출가격이 1개당 5달러로 오른 반면 원유의 수입가격은 변화하지 않았다고 가정하여 봅시다. 이렇게 되면 금년에 반도체 20만개를 수출한 대금으로 수입할 수 있는 원유가 1만 배렬로 늘게 됩니다. 즉, 두 기간 중 국내총생산에 아무런 변화가 없지만 교역조건이 변함에 따라 그 나라 국민의 실질구매력이 증가하는 결과를 초래한 것입니다. 이에 따라 지표경기와 체감경기 간에 괴리가 느껴지는 것입니다.
국민소득 통계는 어떻게 이용되나?
우리는 저축률과 투자율, 경제구조와 같은 용어를 자주 접합고 있습니다. 이와 같은 지표들은 국민소득 통계를 이용하여 구할 수 있습니다. 다시 말해서 국민소득 통계의 부산물인 셈입니다. 이들 지표에 대한 분석을 통하여 국가경제 현황을 차악할 수 있을 뿐만 아니라 다른 나라와의 비교 가능합니다.
먼저 저축률과 투자유에 대하여 알아봅시다. 한 나라 국민이 소비나 저축으로 자유롭게 사용할 수 있는 소득을 '국민총처분가능소득'이라고 합니다. 이는 국민총소득에다 교포송금 등 생산활동과 관계없이 외국으로부터 받은 이전소득을 더하고 무상원조 등의 외국에 지급한 이전소득을 뺀 것입니다. 한 나라의 국민총처분가능소득은 소비와 처축으로 사용됩니다. 저축은 바로 국민총처분가능소득 중 소비되지 않고 남은 부분으로서 투자자금의 원천이 됩니다. 국민총처분가능소득 가운데 저축의 비중을 저축률이라고 합니다.우리나라의 총저축률은 1954년 6%에서 꾸준히 높어져 1988년에 42%로 정점에 도달한 후 하락세로 돌아서 2000년대 이후에는 35% 수준에 머무르고 있습니다.
한 나라 국민이 소비나 저축으로 자유롭게 사용할 수 있는 소득
한편 투자를 국민총처분가능소득으로 나누어 백분율로 나타낸 것을 투자율이라고 합니다. 저축은 국내투자를 충당하고도 남은 경우 외국에 빌려주게 되며 반대로 모자라면 투자자금을 외국에서 조달해 와야 합니다. 이때 외국에 빌려준 자금은 우리나라 저축이 외국에 투자되었다는 의미에서 국외투자라고 부릅니다. 따라서 국내총투자와 국외투자를 합한 총투자는 총저축과 할상 일치하게 됩니다. 이들을 각각 국민총처분가능소득으로 나누어 백분율로 구한 값을 국내총투자율, 국외투자율, 총투자율, 총저축률이라고 하는데 이들 간에는 다음과 같은 관계가 성립합니다.
| 총저축률 | = | 총투자율 | = | 국내총투자율 |
| 국외투자율 |
다음으로 경제구조란 경제의 각 부문이 만들어 낸 부가가치가 국내총생산(GDP)에서 어느정도의 비중을 차지하고 있는지를 말합니다. 한 나라 경제활동의 각 부문은 크게 농림어업, 광공업, 건설업, 전기·가스·수도사업, 서비스업 등으로 분류합니다. 우리나라으 경제구조를 보면 농립어엄이 1970년 28.9%에서 2018년에는 2.0%로 크게 낮아졌으나 같은 기간 중 광공업은 20.4%에서 29.3%로, 서비스ㅓㅂ의 비주은 44.3%에서 60.7%로 높아졌습니다. 이를 통해 우리 경제는 지난 40년 동안 공업화와 서비스화가 꾸준히 진행되고 왔으믕ㄹ 알 수 있습니다. 또 경제구조는 GDP 비중외에 고용비중으로 살펴보기도 합니다.
import numpy as np import pandas as pd import matplotlib.pyplot as plt
year=[1970, 1980, 1990, 2000, 2010, 2018] agri=[28.9, 15.9, 8.4, 4.3, 2.4, 2.0] indus=[20.4, 25.6, 28.0, 29.6, 30.3, 29.3] elec=[1.4, 2.2, 2.2, 2.9, 2.1, 2.1] constr=[5.0, 7.6, 9.5, 6.1, 5.0, 5.9] service=[44.3, 48.7, 51.9, 57.2, 60.1, 60.7] data=pd.DataFrame([year, agri, indus, elec, constr, service]).T data.columns=["연도","농림어업","광공업", "전기,가스,수도업", "건설업","서비스업"] data
| 연도 | 농림어업 | 광공업 | 전기,가스,수도업 | 건설업 | 서비스업 | |
|---|---|---|---|---|---|---|
| 0 | 1970.0 | 28.9 | 20.4 | 1.4 | 5.0 | 44.3 |
| 1 | 1980.0 | 15.9 | 25.6 | 2.2 | 7.6 | 48.7 |
| 2 | 1990.0 | 8.4 | 28.0 | 2.2 | 9.5 | 51.9 |
| 3 | 2000.0 | 4.3 | 29.6 | 2.9 | 6.1 | 57.2 |
| 4 | 2010.0 | 2.4 | 30.3 | 2.1 | 5.0 | 60.1 |
| 5 | 2018.0 | 2.0 | 29.3 | 2.1 | 5.9 | 60.7 |
plt.figure(dpi=100)
plt.bar(data['연도'], data['농림어업'], width=6, data=data.iloc[:,1], label="agriculture, forestry and fishing ")
plt.bar(data['연도'], data['광공업'], width=6, bottom=data['농림어업'], label="mining, industry ")
plt.bar(data['연도'], data['전기,가스,수도업'], width=6, bottom=data['광공업']+data['농림어업'], label="electricity, gas, water industry ")
plt.bar(data['연도'], data['건설업'], width=6, bottom=data['전기,가스,수도업']+data['광공업']+data['농림어업'], label="construction industry ")
plt.bar(data['연도'], data['서비스업'], width=6, bottom=data['건설업']+data['전기,가스,수도업']+data['광공업']+data['농림어업'], label="service")
plt.xticks(data['연도'])
plt.xlabel('Year', weight='bold')
plt.ylabel('%', weight='bold')
plt.legend(bbox_to_anchor=(1.05, 1))
plt.show()
'1인당 국민소득'이 생활수준을 비교하는 정확한 잣대인가?
국민총소득과 1인당 국민소득
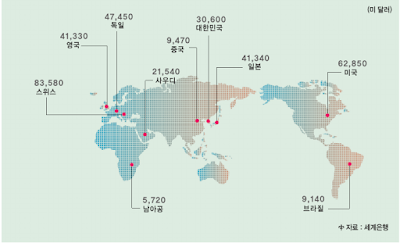
한 나라의 경제력이나 경제규모는 그 나라 국민 전체가 벌어들인 명목국민총소득으로 비교할 수 있지만 한 나라 국민의 생활수준 내지 후생수준을 비교하는 데는 1인당 국민소득이 더 적합합니다. 왜냐하면 국민총소득이 같은 규모의 국가라 하더라고 인구수에 따라 한 사람에게 돌아가는 몫이 큰 차이가 있으며, 국민의 복지 상태는 평균적인 수득수준과 관련이 깊기 때문입니다. 이러한 경우 일반적으로 각국 간 비교를 위햐여 국제적으로 널리 통용되고 있는 미 달러화를 기준으로 환산하고 있습니다.
전 세계적으로 1인당 국민소득 3만 달ㄹ를 넘어선 나라는 그리 많지 않습니다. 선진국 클럽이라 불리는 경제협력개발기구(OECD) 회원국 중 22개국만이 3만 달러를 달성했습니다.
그렇지만 3만 달러 시대에 살고 있다는 것을 체삼하지 못한다는 의견도 적지않고 또 1인당 국민소득은 평균값이기에 소득 불평등을 보여주지 못한다는 한계도 있습니다. 앞으로 더 많은 국민이 경제성장을 체감하고 3만 달러를 넘어 그 이상을 달성하기 위해서는 소득분배와 질적 성장이 이루어져야 합니다. 선진국 사례를 보면 노동력과 자본을 키우는 데만 집중하지 않고 기술혁신과 신성장 산업육성 등을 통해 생산성을 높였을 때 1인당 소득이 4만, 5만 달러를 넘어설 수 있었습니다. 우리 경제가 지속적으로 성장하고 국민 모두가 경제성장의 과실을 나눌 수 있으려면 소득 불평긍을 줄이고 4차 산업혁명 시대에 걸맞는 성장돌력을 찾는 데 힘써야 하겠습니다.
자료: 오용연, '가족과 함쎄 읽는 경제교실', 동아일보 2019년 4월 2일 수정 발췌
예를 들어 세계은행이 3년 평균 환율을 적용하여 발표한 2018년 중 우리나라의 명목 국민총소득(GNI)은 1조 5801억 달러로 스웨덴 5068억 달러의 약 3배이지만 인구는 스웨덴의 약 5배 이기 때문에 1인당 GNI는 우리나라가 3만 600달러로 스웨덴의 5만 5070 달러의 56%에 그치고 있습니다. 한편 우리나라의 1인당 국민총소득이 1960년 100달러에도 미치지 못하였으나 1970년 이후 고도성장에 힘입어 대푝 늘어나 1990년대 중반 1만 달러를 돌파한 후 대체로 상승추세를 보여 2018년 현재 3만 달러를 상회하고 있습니다.
국민소득 통계의 한계
1이낭 국민소득은 한 나라의 국민이 경제적으로 얼마나 잘살고 있는지를 보여주는 유용한 지표인 것은 사실이지만 한계점을 가지고 있고 복지수준을 정확하게 나타내는 척도가 될 수 없습니다.
그 이유로는 첫째로 국민소득이 시장에서 거래되는 재화 및 서비스의 부가가치만을 계산하고 거래되지 않는 재화 및 서비스의 가치는 전혀 포함하지 않고 있다는 점을 들 수 있습니다. 아무리 우리으 경제생활에 유용하게 사용되는 것이라 할지라도 시장에서 거래되지 않으면 국민소득에 포함하지 않습니다. 예를 들어 주부가 가족을 위하여 요리나 빨래, 육아 등을 하는 경우 국민소득에 들어가지 않습니다. 그러나 똑같은 일이라도 음식점이나 세탁소, 보육시설에서 이루어 질때에는 국민소득에 포함됩니다. 따라서 시장이 발달한 나라에서는 국민소득이 늘어나게 됩니다.
밀수, 마약거래, 사채거래와 같은 지하경제 등 비관측경제(non-observed economy)도 당연히 국민소득에 포함되어야 하나 포착이 어려워 빠지게 됩니다. 또한 국민소득에는 행복한 삶을 사는 데 필수적인 여가를 포함하지 않고 있습니다. 여가는 물질적 생산에 직접 기여하지 않지만 여가를 충분히 누릴 수 있는 경우 삶의 질이나 생활수준이 높아진다고 할 수 있습니다. 가령 한 나라의 모든 사람들이 휴일도 없이 일한다면 1인당 국민소득이야 늘어나겠지만 이로 인해 모든 사람들이 행복해진다고 말할 수 없습니다.
국민소들을 계산할 때 포착하기가 어려워 빠진 밀수, 마역거래, 사채거래와 같은 지하경제 등을 말함
1인당 국민소득이 복지수준을 판단하는 데 적합하지 않은 또 다른 이유는 졍제활동과 더불어 발생하는 부작용을 반영하지 않고 있다는 점입니다. 예를 들어 산업화가 진전되면서 오염물질이ㅣ 는ㄹ어나 환경이 파괴되어 복지수준을 저하시키지만 국민ㄴ소득에는 이런 비용이 포함되지 않습니다.즉, 국민경제의 규모가 커지면서 농촌의 황폐화아 도시로의 인구집중, 교통혼잡, 공해, 범죄 증가 등과 같은 외부불경제로 인해 발생하는 효용의 감소를 고려하지 않고 있습니다. 이에 따라 1인당 국민소득이 실제의 복지수준보다 높게 나타날 가능성도 있습니다. 이 밖에 국민소득을 국가 간 비교할 때 적용하는 시장 환율이 한 나라의 통화의 대외적인 실질구매력을 제대로 반영하지 못할 수도 있습니다.
한 나라 국민의 복지수준은 전체 국민의 평균적인 1인당 국민소득 못지 않게 구성원 간 소득격차에 따라서도 크게 다를 수 있습니다. 이는 한 나라 국민의 소득격차가 커지면 못사는 사람의 상대적 박탈감이 더욱 커져 정치·사회적인 문제가 일어날 수 있기 때문입니다. 우리나라도 경제규모가 확대되고 국민의 의식수준이 높아짐에 따라 소득격차의 축소를 통해 삶의 질을 높이려는 욕구가 늘어나고 있습니다.
국민소득의 분배 상태를 측정하는 방법으로 보통 로렌츠곡선과 지니계수를 이용합니다. 로렌츠곡선은 한나라 국민의 소득분배 상태를 파악하기 위해 인구으 누적비율과 소득의 누적점유율과의 관계를 나타낸 곡선을 말합니다. 그림에서 로렌트곡선은 O, L1, L2, O'를 연결한 것입니다. 그리고 OO' 선은 인구의 누적비율과 소득의 누적점유율이 같게 되어 완전균등분배, OTO'선은 그와 반대로 완전불균등 소득분배가 됩니다.
한편 지니계수$\left(\displaystyle\frac{\text{Z의 면적}}{\triangle \text{OTO'의 면적}}\right)$는 로렌츠곡선과 소득의 완전 균등분해를 나타내는 대각선(OO')사이이 면적이 얼마나 되는가를 비율로 나타낸 것입니다. 지니계수가 '0'에 가까울수록소득격차가 적은 것을, '1'에 가까울수록 소득격차가 큰 것을 나타냅니다. 참고로 우리나라의 2018년 지지계수(통계청, 처분가능소득 기준)dms 0.345를 기록하였습니다.
이러한 이유 등으로 1인당 국민소득이 경제복지수준을 정확하게 반영하기 어렵습니다. 이에 따라 국내총새안(GDP))에 여가와 비관측경제의 가치를 더하고 환경오염 관련비용을 공제하는 순경제후생(NEWl Net Economic Welfare)이 제시되기도 하였습니다. 그러나 이 지표도 여가와 비관측경제의 규모를 정화기 산정하기 어렵다는 단점이 있어 기존으 국민소득 통계를 대체하려는 시도가 그다지 진전을 보지 못하고 있습니다. 그렇지만 우리나라를 포함한 많은 국가에서는 기존의 국민소득 통계에서 환경손실분을 공제하는 녹색(green) GDP를 편제하기 위해 준비라고 있습니다.
국내총생산(GDP) 중에서 이를 생산하는 데 발생한 환경손실분을 제거한 후의 GDP
한편 '국민행복지수(GHI: Gross National Happiness)''인간개발지수(HDI: Human Development Index)''더 나은 삶 비수(BLI: Better LIfe Index)' 등과 같은 새로운 지표도 개발되고 있습ㄴ다. 다만 이런 지표들은 아직 여러 면에서 GDP를 대체하는 수준에는 이르지 못하고 있습니다.
GDP는 국제기준에 따라 체계저긍ㄹ 작성되기 때문에 국가 간 상호 비교는 물론 과거와의 비교분석에도 쓰일 수 있짐나 이러한 후생지표는 삶의 만족도와 같은 주관적 항목을 포함하기 때문에 통계의 신뢰성과 일관성을 확보하기 어렵다는 약점이 있습니다. 이 때문에 요즘은 삶의 질을 반영하는 완전히 새로운 지표를 도입하기 보다는 GDP 통계를 보완하는 노력을 하는 것이 대체적인 흐름입니다.
최근에는 인터넷과 스마트폰을 활용한 디지털 경제의 급속한 발전으로 우리의 삶이 풍요로워진 것과 에어비앤비(Airbnb), 우버(Uber) 등 온라인 플랫폼을 통한 숙박, 승차 공유와 같은 공유경제의 효용도 GDP 통계에 충실히 반영하려는 논의도 진행되고 있습니다. 이를 위해서는 통계 편제를 위한 기초 자료의 확충이 필요할 것입니다.
경제성장 나무는 무얼 먹고 자랄까?
경제성장은 어떻게 측정되나?
우리는 '두 마리의 투끼를 다 잡기 어렵다'라는 표현을 자주 씁니다. 경제에서 두 마리 코끼란 '경제성장'과 '물가안정'을 일컫는 말입니다. 이것은 국민경제가 추구하는 중요한 목표입니다. 세계각국이 경제성장을 중요하게 여기는 이유는 국민경제가 성장하면 소득이 증대되고 새로운 일자리가 창출됨으로써 국민의 경제적 후생이 증진되기 때문입ㄴ다. 한 나라의 경제는 통상적으로 시간의 흐름에 따라 점점 커지게 됩니다.
우리나라는 1970년 이후 40년간 연평균 7% 중반의 높은 경제성장을 기록하였습니다. 이러한 고도성장 성과에 대해 외국에서는 독일의 '라인강 기적'에 빗대어 우리나라가 '한강의 기적'을 이루었다고 많이 칭찬하였습니다.
어떤 변수의 값이 2배가 되는 데 얼마나 걸리는지를 아는 방법으로 72법칙이란 것이 있습니다. 즉, 73를 연평균 증가율로 나누어 보면 두 배로 되기까지의 소요연수가 계산됩ㄴ다. 1970 ∼ 2010년간 우리나라는 국내총생산이 연평균 7.6%의 성장율을 기록한 반면 미국은 연평균 2.9% 성장하였습니다. 이 경우 우리나라는 약 10년마다 실질 국내총샌산이 2배씩 증가해 온 반면 미국은 2배 증사하는 데 약 25년이 걸렸다는 이야기 입니다. 높은 경제성장률을 지속적으로 달성한 국가는 경제 규모가 커지는 데 그 만큼 시간이 적게 걸립니다.
다음은 우리나라 경제규모와 GDP성장률에 대한 시계열 자료입니다. 이 자료를 다운받아 그래프를 작성하면 다음과 같습니다.
gdp=pd.read_excel('gdp.xlsx', sheet_name='1', index_col=0)
gdp=gdp.T
gdp.iloc[:,0]=(gdp.iloc[:,0].str.split()).apply(lambda x:float(x[0].replace(",", "")))
gdp=gdp.astype('float')
plt.figure(dpi=100)
plt.plot(list(gdp.index), gdp.values[:,0], )
plt.show()
경제내의 각 활동부문의 부가가치가 얼마나 증가했는지를 알아보는 지표로 흔히 경제성장률을 사용합니다. 경제성장률은 물가요인을 제외한 실질 국내총생신(GDP)이 전년에 비해 얼마나 변동하였는지를 백분율로 나타냅니다.
물가요인을 제외한 실질 국내총생산(GDP)이 전년에 비해 얼마나 변동하였는지를 백분율로 나타낸 것
그러나 경제성장률이 높을수록 좋은 것만은 아닐 수 있습니다. 성장률에는 실제성장률과 잠재성장률이 있습니다. 잠재성장률이란 일정한 시점에서 물가상승을 유발하지 않으면서 경제 내에 주어진 노동과 자본 등을 이용하여 달성할 수 있는 최대 성장률을 말하면, 이는 대체로 수년간의 연평균 성장률과 비슷하며 실제성장률의 장기 추세치로 볼 수 있습ㅂ니다. 따라서 실제의 경제성장률은 호경기에 잠재성장률을 상회하고 불경기에 하회하는 등 잠재성장률의 주위를 맴돈다고 할 수 있습니다. 실제의 경제성장률이 잠재성장률보다 낮으면 한 경제가 최대한 생산할 수 있는 수준이하에서 조업하는 상태이므로 인플레이션을 수반하지 않으면서 총수요(aggregate demand)를 증가시켜 실업률을 낮출 수 있습니다. 이와 반대로 잠재성장률보다 실제성장률이 높으면 경기가 과열되어 물가상승을 촉발시킬 수 있으므로 총수요를 억제할 필요가 있습니다. 여기서 총수요란 모든 경제주체들의 상품과 서비스에 대한 수요의 총계로서 가계부문의 소비지출, 가업부문의 투자지출, 정부부문의 공공지출, 그리고 순수출(수출-수입)을 합한 것입니다. 이처럼 경제성장 속도가 적정한지를 판단하는 데 기준이 되는 잠재성장률은 경제내의 소득이 흐르는 수도관에 비유할 수 있습니다. 이 수도관이 크고 튼튼해야 그 안을 흐르는 소득의 양이 늘어나도 물가상승 압력을 견디어 낼 수 있습니다. 따라서 한 경제가 지속적인 성장을 이루기 위해서는 잠재성장률을 가급적 높은 수준으로 지탱해 나가는 것이 중요합니다.
가계의 소비지출, 기업의 투자지출, 정부의 공공지출, 순수출(수출-수입)을 합한것
경제를 커지게하는 요인은?
경제성장은 나라 전체의 수요와 공급의 양이 지속저긍로 확대되는 것이라고 할 수 있습니다. 이러한 경제성장은 단기적으로 총수요의 변화에 영향을 많이 받습니다. 특히 실제생산이 잠재생산력 수준에 미달한 경우에는 수요증가가 곧바로 경제성장으로 이어집니다. 만일 수요 가운데 수출은 호조를 보였지만 소비 투자 등 국내 수요가 부진한 양극화 현상을 보인다면 총수요 증가가 적어 경제성장은 크지 않게 됩니다. 한편 한 나라의 장기적인 경제성장은 공급측면의 생산증력에 의해 좌우됩니다. 즉, 장기 경제성장은 노동, 자봊, 천연자원 등 생산요소의 트입량이 증가하거나 기술진보가 일어남으로써 가능합니다.
생산요소 가운데 토지를 비롯한 천연자원은 공급이 제한되어 있으므로 노력하여도 생산을 증가시키기 어렵습니다. 따라서 생산요소로 노동과 자본을 중요하게 생각하는데 자본과 노동의 투입 역시 경제가 성숙단계에 이르면 경제성장에 한계를 보입니다.
일반적으로 한 나라의 경제가 성장하면 일자리가 늘어나게 됩니다. 그러나 뉴욕 연방준비은행에 의하면 미국경제는 1990년대 이후 고용 없는 경기회복을 1991년과 2001년 이후 두 차례에 결쳐 경험하였다고 분석하였습니다. 이 가운데 2001년 이후가 더욱 심각하였는데, 그 원인으로 노동시장의 구조가 바뀐 데가 산업구조 변화와 생산성의 향상으로 노동수요가 예전에 비해 크게 줄어든 것을 들고 있습니다.
먼저 노동시장의 구조 변화를 살펴보면 미국은 최근 물가상승률이 현저히 낮아지는 상황에서도 노동비용이 의료보조, 연금굽여 등 간접경비를 중심으로 크게 늘어남에 따라 기업들이 수익감소에 대응하여 고용을 축소하고 있습니다. 또 비용을 절감하고 효율성을 높이기 위해 상용 근로자를 최소화하는 대신 필요할 때 마다 임시직 또는 계약직 근로자를 충원하는 적시(just-in-time)고용 관행이 점차 확산되고 잇으며 인력수요의 국외 외주(global outsourcing)도 늘어나고 있습니다.
산업구조 변화로는 1990년대 후반 이후 관잉투자 등으로 구조적으로 고용이 감소하는 업종이 늘어나고 있습니다. 1990년대까지 미국의 고용증가를 주도하였던 18개 산업 중 전자장비업, 통신서비스업, 기업서비스업, 항공수송업, 주식·상품중개업 등 7개 산업이 2001년 고용감소 산업으로 돌아섰습니다.
이 밖에 IT 혁명에 힘입은 생산성의 향상 역시 기업들이 고용 증대보다 IT 투자를 선호하도록 함으로써 고용부진을 초래하는 원인이 되고 있다고 설명하고 있습니다.
장기 경제성장을 가져오는 또 다른 용이으로 기술진보가 있습니다. 전기나 반도체의 발명처럼 새로운 상품을 만들어 내거나 기술을 개뱔하는 것만 아니라 이미 존재하는 기술을 응용해서 새로운 상품을 개발하는 혁신 등이 그 예가 될 수 있습니다. 재고를 획기저긍로 줄이는 방법을 공나해 낸다거나 노동생산성을 향사시키는 조직관리 방법을 찾아내는 것도 넓은 의미의 기술진보라 할 수 있습니다. 한마리도 기술진보라는 것은 생산성 향상에 기여하는 모든 변화를 포괄하는 개념을 말합니다.
기술진보로 경제성장이 이루어지는 경에는 인구증가나 자본축적에 의한 경제성장과 달리 수확체감의 법칙이 적용되지 않는 특징이 있습니다. 경제성장이 성숙단계로 접어들었다고 하는 선진국들이 꾸준히 성장하고 있는 것은 기술진보 때문입니다. 기술진보가 이루어지면 노동이나 자본의 양이 늘어나지 않아도 장기적으로 경제성장이 지속될 수 있습니다. 이러한 기술진보는 연구개발과 인적자본 투자에 의해 달성될 수 있습니다.
이와같이 장기 경제성장은 노동, 자본과 같은 생산요소의 투입략이 증가하거나 기술진보에 의해 이루어집니다. 그런데 이들 중 어느 요인이 경제성장에 중요한 역할을 하는지를 보면 전후 높은 성장세를 보였던 25년간(1945 ~ 1972년) 미국의 기술진보는 경제성장의 42%를 기여하였다고 합니다. 반면 고도 성장기였던 25년간(1966~1990년) 우리나라와 싱가포르는 기술진보의 기여도가 미국의 절반 이하인 20%에도 못 미치는 것으로 나타나 경제성장의 대부분이 요소투입의 증가에 따라 일어난 것으로 관찰되었습니다. 이에 따라 경제학자 크루그만은 눈부신 경제성장을 이룩했던 동아시아의 기적이 영감에 의한 것이 아니라 땀에 의한 결과라고 비유했습니다.
일반적으로 경제성장은 자본과 노동의 투입략이 성장을 주도하는 단계를 거쳐 기술진보가 성장을 주도하는 단계로 발전하게 됩니다. 우리 경제도 요소 투입에 의한 성장이 한계를 보이고 있음을 감안하여 지속적인 성장을 달성하기 위하여 기술개발에 더욱 힘써야 합니다.




댓글
댓글 쓰기