내용

• 정적분으로 면적 계산
• 극좌표에서의 면적
• 적분에 의한 부피 계산

정적분(Definite Integral)

정적분으로 면적 계산

곡선에 대한 적분 계산으로 면적을 계산할 수 있습니다. 그림 1은 식이 알려진 곡선으로 그 곡선 AB하의 PQNM의 면적을 계산해 봅니다.

그림 1. 곡선의 면적.

그림 1의 지정된 영역 PQNM의 면적은 그 구간 내에 포함된 매우 작은 부분들의 면적을 계산하여 모두 합하는 방식으로 계산될 수 있습니다. 그림 2는 밑면 dx, 높이 dy로서 영역 PQNM 내에 포함된 작은 부분을 나타낸 것으로 각 면적의 합이 지정된 영역의 총 면적이 됩니다.

그림 2. 영역의 부분에 대한 단면적.

위 그림의 면적을 평균 높이 y, 밑면의 길이 dx로 하는 사각형으로 계산할 수 있을까요? 평균 높이를 사용하므로 그림의 윗부분에서 존재하는 부분과 존재하지 않는 부분을 대칭 관계로 고려하면 그 면적을 dx·y로 간주할 수 있습니다. 더구나 dx를 매우 작게 감소시킨다면 대칭 관계로 가정한 부분에서 발생하는 오차가 매우 작아지기 때문에 실제 면적에 더욱 근접할 것입니다. 이 작은 부분의 1개의 면적을 dS로 한다면 다음과 같이 나타낼 수 있습니다.

dS = y·dx

주어진 영역의 총면적은 식 1과 같이 부분 면적의 합으로 표현할 수 있습니다.

$$\begin{equation}\tag{1} \text{총면적}\; S = \int dS = \int y\,dx \end{equation}$$

그러므로 x로 구성된 y의 함수를 안다면 적분에 의해 위 계산을 실행할 수 있습니다. 예를 들어 지정된 영역의 곡선의 함수가 y = b + ax² 라면 이 함수의 적분으로 총 면적을 계산할 수 있습니다.

from sympy import *

a, b, x=symbols("a, b, x")
y=b+a*x**2
inty=integrate(y, x)
inty

$\quad \color{navy}{\frac{a x^{3}}{3} + b x}$

그러나 위에서 사용된 함수는 전체 곡선에 대한 것입니다. 한정된 부분에 대한 면적을 계산하기 위해서는 그 부분의 시작과 끝을 지정해 주어야 합니다. 예를 들면 그림 1의 PQ와 같이 지정된 부분의 면적을 계산하기 위해서는 x의 구간을 M(x₁)에서 N(x₂)으로 한정시켜야 합니다. 적분에서 이러한 구간 설정을 식 2와 같이 표현됩니다.

$$\begin{equation}\tag{2} \int^{x_2}_{x_1} y\, dx = Y_{x_2} - Y_{x_1} \end{equation}$$

위 식과 같이 적분에 한계를 지정한 경우를 정적분(definite integral), 한계가 정해지지 않은 경우를 부정적분(indefinit integral)이라고 합니다. 또한 정적분에 위 첨자로 지정된 한계를 상한(superior limit), 아래 첨자로 지정된 한계를 하한(inferior limit)이라고 합니다.

정적분의 계산은 식 2에서 나타낸 것과 같이 상한까지의 적분에서 하한까지의 적분을 빼주는 것으로 계산합니다. 부정 적분에서 생성되는 상수는 상한과 하한의 차이를 계산하는 과정에서 제거됩니다. 예를 들어 위 함수 y=b+ax₂을 x₁과 x₂ 사이의 정적분일 경우 다음과 같이 계산됩니다.

$$\begin{align} \int^{x_2}_{x_1} y\,dx&=\int^{x_2}_{x_1}(ax^2+b)\, dx\\ &=\frac{a}{3}x^3+bx{\large {|}}^{x_2}_{x_1}\\ &=\frac{a}{3}x^3_2+bx_2-\left(\frac{a}{3}x^3_1+bx_1 \right)\\ &=\frac{a}{3}(x^3_2 -x^3_1)+b(x_2-x_1) \end{align}$$

정적분 계산을 위한 sympy 함수 integrate(식, (변수, 하한, 상한))을 사용합니다.

a, b, x, x1, x2=symbols("a, b, x, x1, x2")
y=b+a*x**2
inty=integrate(y, (x, x1, x2))
inty

$\quad \color{navy}{ - \frac{a x_{1}^{3}}{3} + \frac{a x_{2}^{3}}{3} - b x_{1} + b x_{2}}$

위 식의 각 상수의 값 a = 0.06, b = 10, x₁ = 6, x₂ = 8이라고 하면 다음과 같이 계산됩니다.

inty.subs({a:0.06, b:10, x1:6, x2:8})

 25.92

정적분 계산에 관계된 몇 가지 예들을 계산해 봅시다.

예)
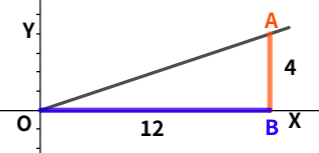
 그림 3의 $\triangle OAB$ 면적?

그림 3. 직선 OA에 대한 면적.

밑면이 12, 높이가 4인 삼각형으로 면적은 24로 쉽게 계산됩니다. 이를 적분으로 계산하기 위해서는 그림에서의 직선 OA에 대한 함수를 사용합니다.

그림에서 (0,0), (12, 4)를 통과하는 직선의 방정식은 다음과 같습니다.

a, b, x, y=symbols("a, b, x, y")
f=a*x+b-y
f1=f.subs({x:0, y:0})
f2=f.subs({x:12,y:4})
sol=solve([f1,f2], (a, b))
sol

{a: 1/3, b: 0}

이 함수에 대해 x=[0, 12] 구간의 적분은 다음과 같습니다.

eq=x/3
integrate(eq, (x, 0, 12))

24

위 계산을 구체적으로 나타내 보면 다음과 같습니다.

$$\begin{align} \int^{12}_{0} \frac{x}{3}\,dx&=\frac{1}{3} \frac{1}{2}\biggr\rvert^{12}_0\\ &=\frac{12^2}{6}-\frac{0^2}{6}\\ &=24 \end{align}$$

위 곡선에서 x=3 과 15사이의 면적이 36임을 확인해 봅니다.

eq=x/3
integrate(eq, (x, 3, 15))

36

예)
  x = x₁과 0사이에 식 $\displaystyle y = \frac{b}{x + a}$에 의해 생성된 영역의 면적을 계산합니다.

a, b, x, x1=symbols("a, b, x, x1")
y=b/(x+a)
integrate(y, (x, 0, x1))

$\quad \color{navy}{- b \log{\left(a \right)} + b \log{\left(a + x_{1} \right)}}$

예)
  $\displaystyle y = b·e^{-x}$에 의한 x=[0, a]구간의 생성되는 영역의 면적을 계산해 봅니다.

a, b, x=symbols("a,b, x")
y=b*exp(x)
integrate(y, (x, 0, a))

$\quad \color{navy}{b e^{a} - b}$

예)
  $pv^n = c$는 완전한 기체의 단열곡선을 나타내는 방정식입니다. 이 식에서 p는 압력, v는 부피, 그리고 c와 n은 상수로서 n = 1.42입니다. 이 곡선이 일정한 부피 $v_1, v_2$사이에 생성되는 면적?

면적은 압력 p와 같습니다.

c, p,v, v1, v2=symbols("c, p,v, v1, v2")
p=c*v**(-1.42)
s=integrate(p, (v, v1, v2))
N(s, 4)

$\quad \color{navy}{ \frac{2.381 c}{v_{1}^{0.42}} - \frac{2.381 c}{v_{2}^{0.42}}}$

예)
  반지름이 R인 원의 면적이 $\displaystyle \pi R^2$임을 적분을 이용하여 증명합니다.

그림 4(a)와 같이 반지름 R인 원은 간격 dr인 링으로 구성된다고 할 수 있습니다.

그림 4. (a)원과 (b)간격 dr인 링의 단면

그림 4(b)와 같이 작은 dr 간격으로 생성되는 링의 단면은 직사각형 형태로서 그 면적 dA는 2πr·dr로 계산됩니다. 그러므로 전체 원의 면적 A는 dA를 반지름 r에 대해 0에서 R의 구간을 적분한 것과 같습니다. 즉,

$$A=\int^R_0 2 \pi r\, dr$$

R, r=symbols("R, r")
dA=2*pi*r
A=integrate(dA, (r, 0, R))
A

$\quad \color{navy}{\pi R^{2}}$

예)
  그림 5는 y = x-x²에 대한 것으로 x축의 양수 부분에서 생성되는 OMN의 평균 높이를 계산해 봅니다. 이 그림에서의 점선의 표시된 사각형의 면적과 곡선에 의한 면적은 동일해야 합니다. 먼저 사각형의 면적을 계산해 봅니다.

그림 5. y = x-x².

이 곡선의 밑면의 길이를 알아보기 위해 식 = 0인 위치를 계산합니다.

x=symbols("x")
y=x-x**2
sol=solve(y, x)
sol

[0, 1]

위 결과에 의하면 x = [0, 1]의 범위를 가지며 밑면의 길이는 1입니다. 이 범위에 대한 식의 정적분은 그림 5 곡선에 의한 면적을 반환합니다.

integrate(y, (x, 0, 1))

$\quad \color{navy}{\frac{1}{6}}$

밑면이 1이므로 평균 높이 $\displaystyle y_{mean} = \frac{1}{6}$이 됩니다. 이 계산으로부터 어느 구간의 평균 높이는 다음과 같이 계산됩니다.

$$y_{mean}=\frac{1}{x_1} \int^1_0 y\,dx$$

예)
  곡선 y = x² - 5를 x축으로 회전시키는 경우 x = 0에서 6까지의 그 곡선에 의해 생성되는 표면적을 계산해 봅니다.

그림 6.(a)곡선$y=x^2-5$ (b) 곡선을 x축으로 회전.

그림 6(b)는 그림 6(a)의 곡선을 x축을 기준으로 회전시킨 경우로서 2개의 원기둥이 생성됩니다. 이 회전체를 매우 작은 dx 구간으로 분리하여 고려하면 반지름은 y값이고 회전체의 둘레 길이는 2πy가 됩니다. 그러므로 dx에 대응하는 면적은 2πydx가 됩니다. [0, 6] 구간에서의 이 식의 정적분으로 총 면적을 계산할 수 있습니다.

x=symbols("x")
y=x**2-5
s=2*pi*y
S=integrate(s, (x, 0, 6))
S

$\quad \color{navy}{84 \pi}$

극좌표에서의 면적

그림 7과 같이 고정된 점 O와 일정한 거리를 가진 r의 관계를 그들이 이루는 각도(θ)의 함수로 나타낼 수 있습니다. 이러한 좌표를 극좌표(polar coordinate)라고 하며 극좌표상에 생성되는 면적을 극좌표의 적분으로 계산할 수 있습니다.

그림 7. 극좌표.

그림 7에서 OAB 사이의 dθ가 극도로 작다면 $\stackrel{\Large{\frown}}{AB}$는 직선에 근접하므로 OAB를 삼각형으로 간주할 수 있습니다. 그러므로 그 작은 삼각형의 면적으로 $\displaystyle \frac{AB}{2}r = \frac{rd\theta}{2}r $에 근접할 것입니다. 이 관계를 적용하여 곡선과 dθ에 대응하는 두 개의 r 사이의 면적(y)은 다음과 같이 계산됩니다.

$$y=\frac{1}{2}\int^{\theta_2}_{\theta_1}r^2\, d\theta$$

반지름 a이고 1라디안의 부분에 대응하는 면적을 계산해 봅니다.

a, th=symbols("a, th")
y=(1/2)*a**2
integrate(y, (th, 0, 1))

$\quad \color{navy}{0.5 a^{2}}$

예)
 다음 극좌표 함수 r = a(1 + cos(θ))에 의해 생성되는 첫 1사분면의 면적을 계산합니다.

그림 8은 위 함수를 그린것으로 첫 1사분면은 0에서 $\displaystyle \frac{\pi}{2}$사이를 의미합니다. 그러므로 위 식에 대한$ \displaystyle \left[0,\;\frac{\pi}{2}\right]$ 구간의 정적분을 의미합니다.

그림 8.r = a(1 + cos(θ)).

a, th=symbols("a, th")
y=(1/2)*a**2*(1+cos(th))**2
integrate(y, (th, 0, pi/2))

$\quad \color{navy}{0.5 a^{2} \left(2 + \frac{3 \pi}{4}\right)}$

위 코드의 함수 y 중 삼각함수를 포함한 부분을 적분하면 다음과 같습니다.

$$\begin{align} \int(1+\cos(\theta))^2\,d\theta&=\int (1+2\cos(\theta)+\cos^2(\theta))\, d\theta\\ &=\theta+2\sin(\theta)+\frac{\theta}{2}+\frac{\sin(2\theta)}{4}+C \end{align}$$

적분에 의한 부피 계산

총면적은 작은 부분의 면적의 합으로 계산하였습니다. 이러한 방식을 전체 부피의 계산에 적용할 수 있습니다. 예를 들어 반지름이 r인 구의 부피를 계산해 봅니다.

그림 9. 반지름 r인 구의 단면.

그림 9는 구의 단면을 나타낸 것으로 폭이 dx이고 높이가 y인 부분은 실제 반지름 y인 원이 됩니다. 그러므로 이 작은 부분의 부피는 πy²이 dx 만큼 있는 것으로 πy²dx로 계산될 수 있습니다. 이 그림에서 y는 반지름 r인 원의 방정식으로 계산되므로 총 부피는 다음과 같이 계산됩니다.

$$\begin{align} y^2&=r^2-x^2\\ V&=2 \pi \int^r_0 y^2 \,dx\\ &=2 \pi \int^r_0 (r^2-x^2)\,dx\\ &=2 \pi \left[\int^r_0 r^2\,dx - \int^r_0 x^2\,dx\right]\\ &=2 \pi \left[ r^2x-\frac{x^3}{3}\right]^r_0\\ &=\frac{4 \pi}{3}r^3 \end{align}$$

다른 예로 곡선 y = 6x²을 X축 [0, 4]구간을 중심으로 회전에 의해 생성되는 회전체의 부피를 계산해 봅니다. 그림 10(a)는 곡선을 나타낸 것으로 이 곡선을 X축을 중심으로 회전하면 그림 10(b)와 같이 나타납니다.

그림 10.(a)y=6x², (b)y=6x²의 회전.

그림 10(a)의 dx 구간의 작은 부분은 회전에 의해 반지름 y이고 높이 dx인 원기둥이 형성되므로 이 생성물의 부피는 πy²dx가 됩니다. 그러므로 이것의 적분에 의해 전체 부피를 계산할 수 있습니다.

a, th=symbols("a, th")
y=pi*6*x
integrate(y, (x, 0, 4))

$\quad \color{navy}{48 \pi}$

N(48*pi, 4)

150.8