미분의 기하학적 의미
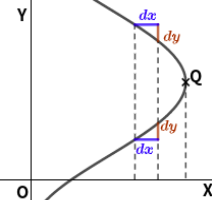
미분 계수는 변화율을 의미하는 것으로서 그림 1과 같이 기하학적으로 나타내면 보다 명확해 집니다.

그림 1에서 곡선 PQR은 X, Y의 축에 대해 작성된 곡선의 일부입니다. 이 곡선에서 점의 가로 좌표가 x이고 세로 좌표가 y인 점 Q가 x가 변할 때 y가 어떻게 변하는지 관찰할 수 있습니다. x가 작은 증분 dx 만큼 증가하면 오른쪽에서 y도 작은 증분 dy 만큼 증가하는 것을 관찰할 수 있습니다. 이것은 이 곡선이 상승 곡선이기 때문에 일어나는 현상입니다. 이 상태에서 dy와 dx의 비율은 곡선이 두 점 Q와 T 사이에서 위로 기울어지는 정도를 측정 한 것입니다. 사실 그림에서 Q와 T 사이의 기울기는 일정하지 않습니다. 즉, Q, T 사이에는 직선이 아닌 곡선이므로 다양한 기울기들 존재하기 때문입니다. 결과적으로 일정한 간격인 dy, dx에 의해 계산된 비율은 각 지점의 변화율에 대한 평균값입니다. 그러나 Q와 T가 직선이라고 간주할 수 있을 만큼 곡선의 작은 부분이라면 비율 $\displaystyle \frac{dy}{dx}$은 QT에서의 곡선의 기울기라고 말할 수 있습니다.
QT가 매우 작다면 점 Q에서의 곡선의 기울기는 그 구간의 기울기 $\displaystyle \frac{dy}{dx}$에 근접하게 되고 그 구간이 지속적으로 작아지면 결국 이 비율은 점 Q에서의 기울기로 간주할 수 있습니다. 이것을 접선의 기울기 (slope of tangent)라고 합니다. 그림 2는 곡선의 기울기와 미분계수의 관계를 나타낸 것으로 각각은 다음과 같습니다.
- 그림 2의 a는 곡선의 작은 부분의 기울기가 45°보다 큰 경우로서 접선의 기울기 $\frac{dy}{dx} \gt 1$
- 그림 2의 b과 같이 특정 지점에서의 기울기가 45°라면 $\displaystyle \frac{dy}{dx}=1$
- 그림 2의 c와 같이 특정 지점에서의 기울기가 45°보다 작으면 $\displaystyle \frac{dy}{dx} \lt 1$

곡선에서의 수평이 이루어지는 지점은 dy = 0이 됩니다. 즉, y의 변화가 없는 경우는 $\displaystyle \frac{dy}{dx}=0$이 됩니다. 그림 2를 일반화하면 그림 3과 같이 나타낼 수 있습니다.
- 그림 3의 a와 같이 곡선이 하향일 경우 dy는 감소하므로 $\displaystyle \frac{dy}{dx} \lt 0$ 로서 음수
- 그림 3의 b와 같이 기울기가 직선일 경우 모든 부분에서 $\displaystyle \frac{dy}{dx}$는 동일하므로 상수
- 그림 3의 c의 경우 기울기는 상승하며 경사도가 증가할수록 계속 증가$\displaystyle \left(\frac{dy}{dx} \gt 0\right)$

그림 3의 c와는 달리 그림 4와 같이 $\displaystyle \frac{dy}{dx}>0 $이지만 x의 증가와 함께 $\displaystyle \frac{dy}{dx}$는 감소하는 경우도 존재합니다.

| 곡선의 형태 | 미분결과 |
|---|---|
| 곡선의 하향 | $\displaystyle \frac{dy}{dx} \lt 0$ |
| 곡선의 수평 | $\displaystyle\frac{dy}{dx}=0$ |
| 곡선의 상향 | $\displaystyle\frac{dy}{dx} \gt 0$ |
그림 5의 a에서와 같이 이 그림의 최소점인 $y_{min}$을 기준으로 곡선이 내려 가는 부분, 수평인 부분, 다시 올라가는 부분으로 구분하여 생각할 수 있으며 각 구간에서의 기울기의 변화는 다음과 같습니다. 곡선의 방향이 하향에서 상향으로 변화되는 지점을 극소값(minimum value)이라고 합니다. 이 극소값은 그 함수에 의한 모든 값 중에 가장 작은 값이라는 의미보다는 지정된 구간에서의 가장 작은 값이라는 의미가 더욱 정확합니다. 그러한 의미에서 곡선이 하향 후 상향의 형상에서 극소값은 존재한다고 할 수 있습니다. 극소값 y를 생성하는 x에서 y의 값의 변화는 없기 때문에 $\displaystyle \frac{dy}{dx}=0$이 성립합니다.
그림 5의 b와 같이 곡선이 처음에 상승하다가 내려가는 경우 상승하는 동안의 $\displaystyle \frac{dy}{dx}>0$이 되며 정상에 도달하면 0이 되고 이후 하강하는 영역에서는 음수가 됩니다. 이렇게 기울기의 부호가 양(positive)에서 음(negative)으로 전환되는 지점에서 y 값을 극대값(maximum value)이라고 하지만 위에서 소개한 최소값과 같이 이 값은 지정한 영역에서의 값을 의미합니다. 다시말하면 y값 중에 가장 큰 값을 의미하는 것은 아닙니다. 극소값의 경우와 같이 극대값 y를 생성하는 x에서 $\displaystyle \frac{dy}{dx}=0$이 성립합니다.

그림 6과 같은 독특한 형태의 곡선에서 $\displaystyle \frac{dy}{dx}$는 항상 양수입니다. 이러한 경향에서도 경사가 가장 가파르지 않는 지점이 존재할 것이며 그 지점의 $\displaystyle \frac{dy}{dx}$가 극소가 될 것입니다.

그림 7의 경우 Q를 기준으로 위쪽의 $\displaystyle \frac{dy}{dx}$는 음수이고 아래쪽은 양수입니다. 점 Q에서 dx는 0에 근접하므로 무한히 커집니다.
위에서 나타낸 여러 그래프들로부터 $\displaystyle \frac{dy}{dx}$는 곡선의 한 지점에서 가파름의 정도를 측정하는 것임을 알 수 있습니다. 몇 개의 예제를 통해 함수의 그래프와 미분 계수의 관계를 알아봅니다.
import numpy as np import pandas as pd from sympy import * import matplotlib.pyplot as plt
예 1)
가장 간단한 경우로 $y = x + b$의 그래프는 그림 8과 같습니다.

이 함수의 그래프는 x와 y에 대해 동일한 스케일을 사용하여 작성됩니다. x = 0을 입력하면 해당 세로 좌표는 y = b가 됩니다. 즉, 곡선은 높이 b에서 y 축과 교차합니다. 여기에서 45°로 올라갑니다. x에 어떤 값을 주든, y는 동일한 기울기로 상승합니다. 즉, 선의 기울기는 1입니다. 이 값은 함수를 미분한 값과 같습니다.
b, x=symbols('b, x')
y=x+b
diff(y, x) #=dy/dx
1
함수의 미분 계수는 상수이므로 그래프의 모든 지점에서 동일한 기울기를 나타냅니다.
예 2)
함수 $y = ax + b$로서 그림 9와 같이 표현됩니다.
그림 8의 경우와 마찬가지로 일정한 높이 b에서 시작됩니다. 이 함수 역시 예 1과 같이 미분 계수는 상수입니다.

a, b, x=symbols('a, b, x')
y=a*x+b
diff(y, x) #= dy/dx
a
함수의 기울기인 상수 a를 임의적으로 $\displaystyle \frac{1}{3}$라 한다면 그림 6.10에서 나타낸 것과 같이 dx는 dy의 3 배가 되는 것입니다.

예 3)
이차 함수 $y = ax^2 + b$는 그림 11과 같이 작성됩니다.

식에서 알 수 있듯이 이 함수의 가장 작은 y 값이 b가 됩니다. 먼저 미분해 보면 다음과 같습니다.
a, b, x=symbols('a,b,x')
y=a*x**2+b
diff(y, x)
2ax
이 결과는 다음과 같이 곡선의 미분 계수를 나타냅니다. 경사도 즉, 기울기는 x에 의존됨을 나타냅니다. 그러므로 상수가 아닙니다.
$$\frac{dy}{dx}=2ax$$그림 11은 위 결과를 잘 반영합니다. 즉, x에 따라 기울기는 증가 또는 감소를 보입니다. 또한 x = 0 인 시작점 P에서 곡선의 경사도가 없습니다. 즉, 수평입니다. x = 0 즉, y 축을 기준으로 왼쪽의 경우 곡선은 왼쪽에서 오른쪽으로 내려갑니다. 그러므로 그 영역에서 $\displaystyle \frac{dy}{dx}$는 음수 값을 가집니다. 반대로 x가 양수 부분에서는 미분 계수는 양수가 됩니다.
예 4)
그림 12는 함수 $\displaystyle \frac{1}{4}x^2+3$을 그래프화 한 것입니다. 이 함수의 미분 계수는 다음과 같습니다.

이제 몇 개의 연속 값들 예를 들어 0에서 5의 범위를 x에 할당합니다. 각 x에 대응하는 원함수의 y값과 미분 계수$\displaystyle \left(\frac{dy}{dx}\right)$를 정리하면 표 6.2과 같습니다.
| x | y | $\displaystyle \frac{dy}{dx}$ |
|---|---|---|
| 0 | 3 | 0 |
| 1 | $\displaystyle 3\frac{1}{4}$ | $\displaystyle \frac{1}{2}$ |
| 2 | 4 | 1 |
| 3 | $\displaystyle 5\frac{1}{4}$ | $\displaystyle 1\frac{1}{2}$ |
| 4 | 7 | 2 |
| 5 | $\displaystyle 9\frac{1}{4}$ | $\displaystyle 2\frac{1}{4}$ |
위의 결과 $\displaystyle \frac{dy}{dx}$를 그래프화하면 그림 13과 같이 나타납니다. 지정된 x 값에 대한 세로 좌표의 높이는 그림 6.12에서 나타낸 곡선의 기울기에 비례한다는 것을 알 수 있습니다.

그림 14와 같이 곡선이 정점에서 급격한 변화를 나타내는 경우 기울기는 양수에서 음수로 급격한 전환이 이루어집니다. 즉, $\displaystyle \frac{dy}{dx}$가 양수에서 음수로 갑작스러운 변화가 나타냅니다.

다음 예제들은 원래의 함수와 그 함수의 미분 계수의 다양한 관계를 나타내기 위한 것입니다.
예 5)
함수 $\displaystyle \frac{1}{2x}+3$의 $x = -1$에서 접선의 기울기와 이 접선과 곡선 $g(x) = 2x^2 + 2$에 의해 생성되는 각도를 계산해 봅시다.
x, b=symbols('x, b', real =True)
y=Rational('1/2')*1/x+3
dydx=diff(y, x)
dydx
$\quad \small \color{blue}{−\frac{1}{2x^2}}$
dydx.subs(x, -1)$\quad \small \color{blue}{−\frac{1}{2}}$
위 결과에 의하면 x = -1에서의 이 함수의 미분계수는 $\displaystyle -\frac{1}{2}$입니다. 이 기울기를 가진 접선의 방정식을 y = ax + b이라고 하면 기울기는 $\displaystyle \frac{dy}{dx} = a = -\frac{1}{2}$가 됩니다. $\displaystyle x = -1,\; y = \frac{5}{2}$가 되므로 이 값을 접선의 방정식에 대입하면 b 값을 계산할 수 있습니다. 접선의 방정식은 다음과 같습니다.
#x=-1에서의 접점 y y_t=y.subs(x, -1) y_t$\quad \small \color{blue}{\frac{5}{2}}$
그러므로 접선은 $\displaystyle y = -\frac{1}{2}x + b$으로 설정할 수 있으며 $\displaystyle \left(-1, \; \frac{5}{2}\right)$좌표를 통과합니다. 이 조건으로 부터 b를 계산할 수 있습니다. sympy 함수 solve() 식의 해를 계산하기 위한 것으로 계산에 적용할 수 있습니다.
y1=-1/2*x+b eq=(y1).subs(x,-1) eq
b+0.5
eq2=Eq(eq, y_t) eq2$\quad \small \color{blue}{b+0.5=\frac{5}{2}}$
b1=solve(eq2, b) b1 #=b
[2.00000000000000]
y1=y1.subs(b, b1[0]) y1
2.0−0.5x
$\displaystyle \left(-1, \frac{5}{2}\right)$에서의 접선의 방정식($y_1$)은 다음과 같습니다.
$$y_1=\frac{1}{2}x+2$$그림 15는 접선의 방정식과 다른 방정식을 작성한 것으로 두 점에서 교차됩니다.

그림 16에서 접선식과 다른 함수 $g(x) = 2x^2 + 2$는 두 점에서 교차됩니다. 각 교차점에서 두 함수가 이루는 각도는 접선식의 기울기와 두 식이 교차된 지점 g(x)의 미분계수(기울기)의 사이에 형성됩니다. 먼저 두 식의 접점은 sympy 함수 solve()를 사용하여 계산합니다.
g=2*x**2+2 y1_g=y1-g y1_g
−2x2-0.5x
meetP=solve(y1_g, x) meetP
[-0.250000000000000, 0.0]
meetP_xy=[(N(i, 3), N(g.subs(x, i), 3)) for i in meetP] meetP_xy
[(-0.250, 2.13), (0, 2.00)]
그림 16과 같이 곡선 g(x)와 접선이 만나는 두 점들에서 생성되는 각은 그 점에서 g(x)의 접선과 $y_1$과의 기울기 차이로 계산됩니다. 각 접선의 방정식의 기울기를 각으로 변환하기 위해 역삼각함수를 사용합니다.
$$\begin{equation} y = \tan(x) \rightarrow \tan^{-1}(y) = x \end{equation}$$이 계산은 sympy함수 atan()를 적용합니다. 또한 sympy의 삼각함수에 관련된 인수들은 각(degree)이 아니라 라디안(radian)이므로 deg(radian)함수를 사용하여 각으로 전환할 수 있습니다.
#접점 x=-0.25 g1=diff(g, x) g1_p1=g1.subs(x, meetP[0]) g1_p1
−1.0
(-deg(atan(-1))--(deg(atan(-1/2)))).evalf(4)
18.44
#접점 x=0 g1_p1=g1.subs(x, meetP[1]) g1_p1
0
(deg(atan(0))--(deg(atan(-1/2)))).evalf(4)
−26.56
예 5)
식 $y = x^2 - 5x + 6$와 좌표 $\; x = 2, \; y = -1$를 통과하고 y의 접선이 되는 직선과의 접점을 계산합니다.
이 예의 경우 다음 과정에 의해 계산할 수 있습니다.
- y의 미분계수 $\displaystyle \; \frac{dy}{dx}$
- 좌표 (2,-1)를 통과하는 직선 g(x) = ax + b라고 하면이 그 좌표(2, -1)을 대입하여 b를 a로 정리할 수 있습니다.
- 함수 y의 미분계수가 좌표(2, -1)을 통과하는 직선의 기울기가 됩니다. 즉, $\displaystyle \; \frac{dy}{dx} = a$
- y = g(x)에서 x를 계산하고 그에 대응하는 y값을 발견합니다.
이 과정을 코드화하면 다음과 같습니다.
a, b, x=symbols("a, b, x", real=True)
y=x**2-5*x+6
g=a*x+b
dydx=diff(y, x)
dydx
2x−5
위의 결과는 함수 y의 미분계수입니다. 이 값은 변수 x에 의존합니다. 다음 과정은 g(x)에 (2,-1)을 대입하여 b를 a의 형태로 전환합니다.
b1=solve(Eq(g.subs(x, 2), -1),b) b1
[-2*a - 1]
g=g.subs(b, b1[0]) g
ax−2a−1
g(x)의 기울기를 y의 미분계수로 치환합니다. 이 과정에 의해 g(x)의 상수 a와 b는 모두 변수 x로 치환됩니다.
g=g.subs(a, dydx) g
x(2x−5)−4x+9
최종적으로 y = g(x)를 계산합니다.
x_con=solve(Eq(y, g), x) x_con
[1, 3]
y_con=[y.subs(x, i) for i in x_con] y_con
[2, 0]

댓글
댓글 쓰기