활성함수

내용

1. 시그모이드함수(Sigmoid function)
2. ReLU 함수
3. 하이퍼볼릭탄젠트함수

활성함수(activation function)

활성함수는 가중치 합계를 계산하고 여기에 편향을 추가하여 뉴런의 활성화 여부를 결정합니다. 즉, 이 함수를 통과하면서 선형함수의 결과를 비선형으로 전환됩니다. 선형함수는 입력과 출력사이에 상수배의 관계를 의미합니다. 즉, 동일한 변화를 가지는 것으로 직선의 형태를 보이지만 비선형은 직선으로 표시할 수 없습니다. 선형함수의 반복은 그 관계를 변화시킬 수 없으므로 입력 층에 대한 신호의 변화를 명확히 하기 위해 비선형 함수 즉, 활성함수를 사용하여야 합니다. 결과적으로 활성화 함수는 미분가능한 비선형 결과를 반환합니다. 활성화함수는 다양한 종류가 있으며 그 중 일반적으로 사용하는 몇 가지를 살펴보면 다음과 같습니다.

시그모이드함수(Sigmoid function)

시그모이드 함수는 식 1과 같으며 모든 값은 (0, 1) 구간내로 변환합니다.

$$\begin{equation}\tag{1} \begin{aligned}&\text{sigmoid} ;\\ & f(x)=\frac{1}{1+\exp(-x)} \end{aligned} \end{equation}$$

인공 뉴런은 임계값을 기준으로 활성화 여부를 결정합니다. 입력이 임계값을 초과할 때 값 1을 취하고 반대의 경우는 0을 취합니다. 딥러닝은 그라디언트 기반 학습으로 임계값 단위에 대한 매끄럽고 미분 가능한 근사값의 출력이 가능하여야 합니다. 시그모이드 함수는 이러한 조건을 충족하는 함수입니다. 그러나 입력이 0에 가까울 때 시그모이드 함수는 선형 변환에 접근합니다.

x=torch.arange(-10, 10, 0.001, requires_grad=True)
y=torch.sigmoid(x)

plt.plot(x.detach().numpy(), y.detach().numpy())
plt.xlabel("x", size=11, weight="bold")
plt.ylabel("sigmoid(x)", size=11, weight="bold")
plt.show()

이 함수의 미분은 식 2과 같습니다.

$$\begin{align}\tag{2}\frac{d}{dx}\text{sigmoid(x)}&=\frac{\exp(-x)}{(1+exp(-x)))^2}\\&=\text{sigmoid(x)}(1-\text{sigmoid(x)})\end{align}$$

시그모이드 함수의 도함수는 아래에 표시됩니다. 입력이 0일 때 시그모이드 함수의 도함수는 최대 0.25에 도달합니다. 입력이 어느 방향으로든 0에서 발산함에 따라 도함수는 0에 접근합니다.

y.backward(torch.ones_like(x), retain_graph=True)

plt.plot(x.detach().numpy(), x.grad.detach().numpy())
plt.xlabel("x", size=11, weight="bold")
plt.ylabel("grad of sigmoid", size=11, weight="bold")
plt.show()

위 그래프에서 나타낸 것과 같이 이 함수는 입력의 절대값이 클수록 도함수값이 0으로 수렴되므로 학습 중지의 가능성이 증가할 수 있습니다. 즉, 이러한 경향은 역전파 과정에서 수행하는 미분 연산을 방해하는 요인이 됩니다. 다수의 은닉층이 존재할 경우 역전파 과정에서 실행되는 변화도 (미분)는 0에 접근하므로 가중치 W의 학습이 이루어지지 않게 됩니다. 이러한 현상을 기울기 소실 (Vanishing Gradient) 라고 합니다. 이러한 이유로 은닉층에 시그모이드 함수를 적용하는 것은 지양됩니다.

ReLU 함수

구현의 단순성과 다양한 예측 작업에 대한 우수한 성능으로 인해 가장 인기 있는 선택은 ReLU(Rectified Linear Unit)입니다. ReLU는 매우 간단한 비선형 변환을 제공합니다. 요소 x가 주어지면 함수는 해당 요소의 최대값과 최소값을 0으로 정의합니다.

$$\begin{align}\tag{3} f(x)&=\begin{cases} 0 & x\lt 0\\ x & x\ge 0 \end{cases}\\ReLU(x) &= \text{max(0, x)} \end{align}$$

비공식적으로 ReLU 함수는 해당 활성화를 0으로 설정하여 양수 요소만 유지하고 모든 음수 요소를 버립니다. 이 함수의 형태는 다음과 같습니다.

y_relu=torch.relu(x)
x.grad.data.zero_()
y_relu.backward(torch.ones_like(x), retain_graph=True)

plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.title("ReLu")
plt.plot(x.detach().numpy(), y_relu.detach().numpy())
plt.xlabel("x", size=11, weight="bold")
plt.ylabel("ReLU(x)", size=11, weight="bold")
plt.subplot(1,2,2)
plt.title("grad of ReLU")
plt.plot(x.detach().numpy(), x.grad.detach().numpy())
plt.xlabel("x", size=11, weight="bold")
plt.ylabel("grad of ReLu", size=11, weight="bold")
plt.show()

입력이 음수이면 ReLU 함수의 도함수는 0이고 입력이 양수이면 ReLU 함수의 도함수는 1입니다. 입력이 정확히 0과 같거나 작은 경우 ReLU 함수는 기울기 소실에 직면하게 됩니다. 미분할 수 없습니다. 이러한 경우, 우리는 기본적으로 왼쪽 도함수를 사용하고 입력이 0일 때 도함수가 0이라고 말합니다. 그러나 대부분의 경우 입력이 실제로 0이 되는 경우는 드물기 때문에 이 문제를 피할 수 있습니다. 보다 적극적으로 다음 식과 같이 ReLU 함수를 수정한 parameterized ReLU(pReLU)를 적용하여 이 문제에 대한 가능성을 축소시킬 수 있습니다.

pReLU(x) = max(0, x) + α min(0, x)

y_prelu=torch.prelu(x, torch.tensor(0.2))
x.grad.data.zero_()
y_prelu.backward(torch.ones_like(x), retain_graph=True)

plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.title("PReLu")
plt.plot(x.detach().numpy(), y_prelu.detach().numpy())
plt.xlabel("x", size=11, weight="bold")
plt.ylabel("ReLU(x)", size=11, weight="bold")
plt.subplot(1,2,2)
plt.title("grad of PReLU")
plt.plot(x.detach().numpy(), x.grad.detach().numpy())
plt.xlabel("x", size=11, weight="bold")
plt.ylabel("grad of ReLu", size=11, weight="bold")
plt.grid(True)
plt.show()

하이퍼볼릭탄젠트함수(Hyperbolic tangent function, tanh)

식 4의 형태를 가진 하이퍼블릭 탄젠트함수(tanh)는 시그모이드 함수와 유사하지만 변환하는 값의 범위가 (-1,1)로서 더 넓어집니다.

$$\begin{equation}\tag{4} tanh(x)=\frac{1-e^{-x}}{1+e^{-x}} \end{equation}$$

x=torch.arange(-10, 10, 0.001, requires_grad=True)
y=torch.tanh(x)

plt.figure(figsize=(7, 4))
plt.plot(x.detach().numpy(), y.detach().numpy())
plt.xlabel("x", size=12, weight="bold")
plt.ylabel("tanh(x)", size=12, weight="bold")
plt.grid(True)
plt.show()

위 그림과 같이 x축의 양끝으로 이동할수록 기울기 소실 현상이 나타납니다. 그러나 시그모이드 함수와는 달리 0을 중심으로 대칭되어 변화 영역이 넓어지므로 기울기 소실 현상이 감소됩니다. 이러한 이유로 비선형을 위한 활성함수로 시그모이드 함수보다 많이 사용됩니다.

tanh()의 미분은 다음과 같습니다.

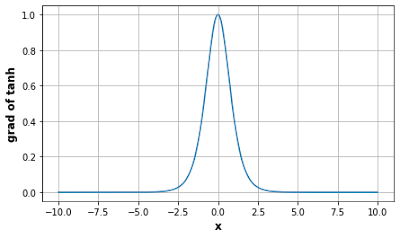
$$\frac{d}{dx} tanh(x) = 1- tanh^2(x)$$

tanh 함수의 도함수의 형태는 다음과 같습니다. 입력이 0에 가까워짐에 따라 tanh 함수의 도함수는 최대값 1에 접근합니다. 그리고 시그모이드 함수에서 보았듯이 입력이 어느 방향으로든 0에서 멀어질수록 tanh 함수의 도함수는 0에 접근합니다.

y.backward(torch.ones_like(x), retain_graph=True)

plt.figure(figsize=(7, 4))
plt.plot(x.detach().numpy(), x.grad)
plt.xlabel("x", size=12, weight="bold")
plt.ylabel("grad of tanh", size=12, weight="bold")
plt.grid(True)
plt.show()