확률의 개요

확률이란...

확률은 미래에 발생할 사건에 대한 믿음의 측정값입니다. 어떠한 사건에 대해 그 사건이 일어날 빈도수를 전체사건에서 차지하는 비율로 나타낼 수 있습니다.
확률은 통계의 기본이 되며 일상에서 많은 경우를 접하고 있습니다. 그러나 확률을 정의하는 것은 많은 사람들에게는 새로운 작업이 될 수도 있습니다. 그러나 이것은 일상에서 접하는 것을 서술하는 것으로 사실 새로운 것은 아닙니다.

1. 용어

이러한 확률을 다루기 위해서 몇가지 알아야할 용어가 있습니다.

- 확률실험(random experiment, 시행)
실험결과를 예측할 수 없는 실험을 말하며 실험결과를 알 수 없다는 것은 실험의 모든 시행의 가능성이 동일하다고 할 수 있습니다. 예를들어 동전던지기에서 앞과 뒤가 나올 확률은 동일합니다. 이러한 실험을 확률실험이라고 합니다.

- 표본공간(sample space)와 원소(element)
확률실험의 각 결과를 원소라 하며 그 실험의 모든 결과를 모아 놓은 공간을 표본공간이라고 합니다. 주사위 던지기 실험 역시 각 눈의 값이 나올 확률은 동일하므로 확률실험이며 이 실험에서 나올 수 있는 결과(사건)은 1, 2,3 ,4,5 ,6 입니다. 이 모든 사건들의 모임을 표본공간이라고 하고 이 실험에서 표본공간(S)은
S={1,2,3,4,5,6}
이며 각 값들을 원소라고 합니다.

- 사건(event) 또는 집합(set)
확률실험에서 관심의 대상이 되는 원소들의 모임을 사건 또는 집합이라고 합니다. 특히 확률이 정의된 집합을 사건이라고 합니다.

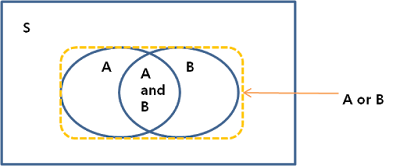
- 벤다이어그램(Venn Diagram) : 집합간의 관계를 그림으로 나타낸 것입니다.

그림 1 벤다이어 그램 

- 전체집합(Universe set) : 샘플공간과 같으며 실험에서 발생하는 모든 원소들의 집합입니다. 그림 1에서 S

- 공집합(Empty set) : 원소가 하나도 없는 집합 ($\emptyset$)
- 합집합(Union) :  각 집합에 속한 모든 원소들의 집합 (A or B= A &\cup$ B).
 집합 A와 집합 B의 합집합의 확률: $P(A \cup B) = P(A) + P(B)+ P(A \cap B)$
- 교집합(Intersection): 두 집합에 공통으로 속한 원소들의 집합(A and B = A $\cap$ B)
집합 A와 집합 B의 합집합의 확률: $P(A \cap B) = P(A) \times P(B)$이지만 이 경우는 사건 A와 B가 독립일 경우에 해당됩니다.
- 여집합(complement): 전체 집합에서 특정 집합에 속한 원소들의 제외한 모든 원소 집합 ($A^c)
- 부분집합(subset): 특정 집합의 원소들을 다른 집합에 모두 속하는 경우를 부분집합이라고 합니다. 즉, 집합 C는 집합 A의 부분집합이라고 하면 C의 모든 원소들은 A에 포함되며 다음과 같이 나타냅니다. C $\subset$ A
- 상호 배타적 또는 독립적(mutually exclusive, disjoint, independent) : 두사건의 교집합이 공집합인 경우 (A $\cap$ B = \emptyset$)
- 분배법칙(Distribution Laws)
$A \cup (B \cap C) = (A \cup B) \cap (A \cup B)$
$A \cap (B \cup C) = (A \cap B) \cup (A \cap B)$

-드모르간 법칙(DeNorgan's law)

$(A \cup B)^c = A^c \cap B^c, \quad (A \cap B)^c = A^c \cup B^c$

표본공간 S인 실험에서 임의의 사건 A에 대해 아래 조건을 만족하는 P(A)를 A의 확률(Probability)이라 정의 합니다.

- $P(A) \geq 0$ 즉, 모든 사건의 확률은 0보다 크거나 같다.
- P(S) =1
- 여러사건 $ A_1, A_2, \cdots , A_k$가 상호 배타적 또는 독립적이라면 그 사건들의 합은 다음과 같이 나타낼 수 있습니다.
$P(A_1 \cup A_2 \cup, \cdots, \cup A_k)= \sum^k_{i=1} P(A_i)$

2. 확률계산 

 확률을 계산하기 위해서는
1) 전체 공간 즉, 표본 공간을 정의하고
2) 표본공간의 각 원소들에 적절한 확률값을 할당합니다.
3) 특별한 대상사건을 정의합니다.
4) 그 사건의 각 원소의 확률을 더해 사건의 확률을 정의합니다.

예1) 동전 3개를 던지는 확률실험(시행)에서 앞면이 두개 이상 나올 확률을 구해봅니다.
1) 표본공간:
>>> x=["H", "T"]
>>> S=[(i,j,k) for i in x for j in x for k in x]
>>> S
[('H', 'H', 'H'),
 ('H', 'H', 'T'),
 ('H', 'T', 'H'),
 ('H', 'T', 'T'),
 ('T', 'H', 'H'),
 ('T', 'H', 'T'),
 ('T', 'T', 'H'),
 ('T', 'T', 'T')]
2) 위의 표본공간의 각 원소의 확률은 동일하므로 1/8입니다.
3) 두개이상이 앞면이 나오는 사건은 다음과 같습니다.
>>> A=[i for i in S if i.count("H") >= 2]
>>> A
[['H', 'H', 'H'], ['H', 'H', 'T'], ['H', 'T', 'H'], ['T', 'H', 'H']]
4) 그러므로 사건 A의 확률은$ 4 \times\frac{1}{8}=\frac{1}{2}$ 입니다.

예 2) A와 B가 게임을 하는데 평균 전적이 A가 2/3입니다. 이 조건에서 두 게임을 할 경우 A가 적어도 한번 이길 확률?
이 문제에서 알수 있는 사전 정보는 A, B의 각각의 확률이 $P(A)=\frac{2}{3}, \; P(B)=\frac{1}{3}$ 이라는 것입니다. 두 게임을 할 경우
1) 표본공간
>>> x=["A", "B"]
>>> S=[[i,j] for i in x for j in x]
>>> S
[['A', 'A'], ['A', 'B'], ['B', 'A'], ['B', 'B']]
2) S 각 원소의 확률은 다음과 같습니다.
$2/3\cdot 2/3=4/9, \; 2/3\cdot 1/3=2/9,\; 1/3\cdot 2/3=2/9,\; 1/3\cdot 1/3=1/9$
3) A가 최소 한번 이기는 사건
>>> A=[i for i in S if i.count("A") >= 1]
>>> A
[['A', 'A'], ['A', 'B'], ['B', 'A']]
4) 위 사건의 확률은 4/9+2/9+2/9 =8/9 입니다.
또한 이 사건은 전체에서 A가 모두 질 확률을 제외한 경우와 같으므로 1-1/9=8/9와 같이 계산될 수 있습니다.

위 예에서 3전 2선승제에서 A가 이길 확률은 ?
>>> x1=[2/3, 1/3]
>>> S1= [[i,j, k] for i in x1 for j in x1 for k in x1]
>>> S2=[i for i in S1 if i.count(2/3) >= 2]
>>> S3=[i*j*k for i,j,k in S2]
>>> np.sum(np.array(S3))
0.7407407407407407

위와 같이 확률을 계산하는데이 있어 전체 원소들의 빈도 또는 갯수를 알아내는 것으로 시작됩니다. 이 경우 순열, 조합등 다음과 같이 계산할 수 있습니다.
- 곱의 법칙 : 두개의 독립된 사건인 m과 n의 시행에서 이루어질수 있는 경우의 수는 mn입니다.
예) 2개의 주사위를 시행할 경우 나올 수 있는 경우의 수는
>>> A=[[i, j] for i in range(1, 7) for j in range(1, 7)]
>>> A
[[1, 1],
 [1, 2],
 ...
 [6, 5],
 [6, 6]]
>>> len(A)
36
>>> 6*6
36
- 순열(permutation) : 순서를 고려하여 n개의 서로 다른 원소들에서 p개를 선택하는 경우의 수는 다음과 같이 계산됩니다.
$_nP_r= \frac{n!}{(n-r)!}$
예) 4개의 서로 다른 숫자로 된 암호를 찾기 위한 경우의 수. 이것은 0~9까지의 숫자중에서 4개의 숫자를 선택하는 것으로 순서를 생각하는 것이므로 한번 선택된 수는 다음에 선택되서는 안되지요. 그러므로 처음에 올 수의 경우 부터 차례로 10, 9, 8, 7 이고 그 이후에는 계산에서 제외되어야 합니다. 즉 10!/(10-4)!이 되어야 합니다.
 (!를 factorial이라고 하는데 python의 math 모듈의 factorial() 함수로 계산됩니다.)
>>> math.factorial(10)/math.factorial(6)
5040.0

- 조합(combination): 순서를 고려하지 않고 n개에서 서로다른 p개를 선택하는 경우의 수는 다음과 같이 계산됩니다.
$\left( \begin{array}{rr} n \\ r \end{array} \right)=_nC_r= \frac{n!}{r!(n-r)!}$
위의 4개의 암호 숫자를 찾는 경우에서 순열의 경우는 1234와 4321은 다른 것으로 간주하지만 조합의 경우는 순서를 고려하므로 이 둘을 같은 것으로 간주합니다. 그러므로 순열의 경우에서 선택한 수의 배열의 경우의 수를 고려해야합니다. 그러므로 결과는 다음과 같습니다.
>>> math.factorial(10)/(math.factorial(6)*math.factorial(4))
210.0

- 위의 조합 계산은 이항인 경우를 계산 한 것입니다. 만약 대상이 다항일 경우에 이 공식을 적용할 수 있을까요? 다음 예를 봅시다.
예) 학생 20명이 MT를 가서 방을 4개를 배정받는데 각 방의 인원수는 6, 4, 5, 5 명입니다. 방을 배정할 수 있는 경우의 수는 다음의 생각으로 부터 계산될 수 있습니다.
20 중에 6명을 뽑는 조합 $\times$ 14명에서 4명을 선택하는 조합 $\times$ 10명에서 5명 선택 조합 $\times$ 5명에서 5명을 선택하는 조합
>>> x=[[20,6],[14,4], [10,5]]
>>> c1=[math.factorial(x[i][0])/(math.factorial(x[i][1])*math.factorial(x[i][0]-x[i][1])) for i in range(len(x))]
>>> np.prod(np.array(c1))
9777287520.0
즉,
$\frac{20!}{6! 14!}\frac{14!}{4! 10!}\frac{10!}{5! 5!}\frac{5!}{5! 0!}=\frac{20!}{6!4!5!5!}=\left( \begin{array}{rr} 20 \\ 6\;4\;5\;5 \end{array} \right)$
위를 일반화하면 서로 다른 원소 n을 그룹의 원소의 수가 각각 n1, n2, ..., n_r일 경우 다음과 같은 식이 성립됩니다.
$\left( \begin{array}{rr} n \\ n_1\;n_2\cdots5\;n_r \end{array} \right)=\frac{n!}{n_1!n_2!\cdots n_r!}$