Gamma , Chi square and F distribution

Contents

1. Gamma Distribution
   1. Gamma function
   2. Gamma distribution
2. Chi-square distribution
3. F distribution

Gamma Distribution

Since the probability is the ratio of the target cases to the total number of cases, it is important to calculate the total number of cases in calculating the probability. For discrete variables, the total number of cases is calculated using factorial. In the case of continuous variables, the factorial cannot be calculated directly because random variables are not countable. Instead, an integral expression corresponding to factorial is used, which can be replaced with gamma function. Therefore, the gamma distribution based on the gamma function is a distribution related to the exponential distribution and the normal distribution and is used in various fields.

Gamma function

The gamma function is expressed as Γ(x) and has the form of a factorial function in the realm of natural numbers, and is defined as Equation 1 for discrete and continuous variables, respectively.

$$\begin{align}\tag{1} \Gamma(n)&=(n-1)! , \quad\quad n \in \{1,2,3, \cdots \}\\ &=(n-1)\Gamma(n-1)\\ &=\int^n_0 x^{n-1}e^{-x} ,\quad n > 0 \end{align}$$

Example 1)
  Calculate the factorial and gamma function of discrete and continuous variables with n=10.

Factorial can be calculated with factorial() function of numpy or scipy's math module, and the above gamma function can be calculated with scipy.special's gamma() function. Also, this calculation can be performed using the symbol() function and the intergrate() function of the sympy package.

import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt 
from sympy import *
from scipy import stats
from scipy import special

np.math.factorial(10-1)

362880

special.gamma(10)

362880

x=symbols('x')
g=x**9*exp(-x)
gamma=g.integrate((x, 0, oo))
gamma

362880

The form of the gamma function is as follows.

plt.figure(figsize=(7, 4))
rng=np.arange(0, 4, 0.1)
gam=[special.gamma(i) for i in rng]
plt.plot(rng, gam)
plt.xlabel("n", fontsize="13", fontweight="bold")
plt.ylabel(r"$\Gamma(n)$", fontsize="13", fontweight="bold")
plt.show()

Figure 1.

Gamma distribution

Gamma distribution is a probability distribution and the total number of cases is calculated using the gamma function. As a result, the gamma distribution is defined as a distribution inversely proportional to the gamma function as follows.

The probability density function (PDF) of a continuous random variable following a gamma distribution with parameters α (total number of occurrences) and λ (average number of occurrences) is defined as Equation 2.

$$\begin{equation}\tag{2} f(x)=\frac{\lambda^{\alpha}x^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}, \quad \alpha>0, \; \lambda >0, \; x>0 \end{equation}$$

A continuous random variable that follows this distribution is expressed as

$$X \sim \text{Gamma}(\alpha, \lambda)$$

If α = 1, the PDF is as follows, and this form is the same as the exponential distribution.

$$f(x) =\lambda e^{-\lambda x}$$

So Γ(1, λ)= Exponential(λ). Generalizing this relationship, it can be said that the sum of $\alpha$ random variables following an exponential distribution follows Γ(α, λ).

Gamma distribution can be calculated using the scipy.stats.gamma() class for various statistics. Typically, stats.gamma.pdf(x, a, loc=0, scale=1) is used to calculate the probability of each random variable. This function calculates the following probability density function.

$$f(x)=\frac{x^{a-1} \exp(-x)}{\Gamma (a)}$$

The a in this function means α, and by default, the parameters λ, loc, and scale of this function are set to 1, 0, and 1, respectively. Therefore, if λ is not 1, the scale of the stats.gamma.pdf() function should be set to $frac{1}{\lambda}$. That is, λ is a constant that is inversely proportional to the standard deviation of the distribution.

Figure 2 is the gamma distribution according to the change of α and λ.

plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
rng=np.arange(1, 10, 2)
for i in rng:
    gam=[stats.gamma.pdf(j, i) for j in np.arange(1,15, 0.1)]    
    plt.plot(np.arange(1,15, 0.1), gam, label="Gamma("+str(i)+", 1)")
plt.xlabel("n", fontsize="13", fontweight="bold")
plt.ylabel(r"$Gamma(n)$", fontsize="13", fontweight="bold")
plt.title(r'Gamma distribution & $\alpha$ ', fontsize="14", fontweight="bold")
plt.legend(loc="best")
plt.subplot(1,2,2)
rng=np.arange(1, 10, 2)
for i in rng:
    gam=[stats.gamma.pdf(j, 5, scale=1/i) for j in np.arange(1,15, 0.1)]
    plt.plot(np.arange(1,15, 0.1), gam, label="Gamma(5, "+str(i)+")")
plt.xlabel("n", fontsize="13", fontweight="bold")
plt.ylabel(r"$\Gamma(n)$", fontsize="13", fontweight="bold")
plt.title(r'Gamma distribution & $\lambda$', fontsize="14", fontweight="bold")
plt.legend(loc="best")
plt.show()

Figure 2. Effect of $\alpha$ and $\lambda$ on gamma distribution.

As shown in Figure 2, when α is 1, the distribution is exponential, and as α increases, the distribution approximates to the normal distribution. Also, the λ adjustment indicates the form of a symmetric distribution (normal distribution). In other words, the gamma distribution can be said to be the basic form of calculating probability for continuous variables.

Using the probability density function of the distribution, the mean and variance are derived as Equations 3 and 4, respectively.

$$\begin{align}\tag{3} E(X)&= \int^\infty_0 x\frac{\lambda^{\alpha}x^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)} \, dx\\&= \int^\infty_0 \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha}e^{-\lambda x}\, dx\\& =\int^\infty_0 \frac{\alpha \lambda^{\alpha+1}}{\Gamma(\alpha+1) \lambda} x^{\alpha}e^{-\lambda x}\, dx\\&=\frac{\alpha}{\lambda}\int^\infty_0 f(x)\, dx\\&=\frac{\alpha}{\lambda}\end{align}$$ $$\begin{align} E(X^2)&=\int^\infty_0 x^2\frac{\lambda^{\alpha}x^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)} \, dx\\ &=\int^\infty_0 \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha+1}e^{-\lambda x}\, dx \\ &=\int^\infty_0 \frac{\alpha \lambda^{\alpha+2}}{\Gamma(\alpha+1) \lambda^2} x^{\alpha+1}e^{-\lambda x}\, dx\\ &=\frac{\alpha(\alpha+1)}{\lambda^2}\int^\infty_0 f(x)\, dx\\ &=\frac{\alpha(\alpha+1)}{\lambda^2} \end{align}$$ $$\begin{align}\tag{4} Var(X)&=E(X**2)-(E(X))**2\\&=\frac{\alpha(\alpha+1)}{\lambda^2}-\left(\frac{\alpha}{\lambda}\right)^2\\&=\frac{\alpha}{\lambda^2} \end{align}$$

from sympy import gamma
a, l, x=symbols("alpha, lambda, x", positive=True)
f=l**a*x**(a-1)*exp(-l*x)/gamma(a)
f

$\qquad \color{blue}{\displaystyle \frac{\lambda^{\alpha} x^{\alpha - 1} e^{- \lambda x}}{\Gamma\left(\alpha\right)}}$

E=simplify(integrate(x*f,(x, 0, oo)))
E

$\qquad \color{blue}{\displaystyle \frac{\alpha}{\lambda}}$

E2=simplify(integrate(x**2*f,(x, 0, oo)))
E2

$\qquad \color{blue}{\displaystyle \frac{\alpha \left(\alpha + 1\right)}{\lambda^2}}$

var=E2-E**2
simplify(var)

$\qquad \color{blue}{\displaystyle \frac{\alpha}{\lambda^{2}}}$

Example 2)
  The sample analyzer contains two fuses, including a spare. In general, these fuses should last up to 50 hours. However, the specification from the fuse manufacturer reports that it turns off once every 100 hours. What is the probability that both fuses will not hold for 50 hours?

The average number of events over a given period is λ = 0.01 hour^-1 . In addition, if the time elapsed until the second fuse fails is X as a random variable, it can be expressed as a gamma distribution with the total number of occurrences &alpha=2; and λ as parameters. in other words,

$$X \sim \text{Gamma} \left(2,\, \frac{1}{100} \right) $$

This example is equivalent to calculating a random variable P(X ≤ 50).

round(stats.gamma.cdf(50, 2, scale=1/0.01),4)

0.0902

Chi-square distribution

The binomial distribution applies to two mutually exclusive (independent) variables and can be converted to an approximately normal distribution. A distribution that can be extended to two or more independent variables following this binomial and normal distribution is called a chi-square distribution. For example, the chi-square distribution is used as a distribution to infer a certain outcome by listing the data of students included in each class, the results of treatment for patients, etc. This chi-square distribution is a special case of the gamma distribution function and is expressed as Equation 5.

$$\begin{align}\tag{5} &\chi ^2(k) \sim \Gamma(\alpha=k, \lambda=2)\\ & k: \text{positive integer and degrees of freedom (df)} \end{align}$$

The chi-square distribution is a distribution of the squared values of several standard normal random variables, and the shape of the distribution varies depending on the degrees of freedom (the number of normal distributions). For example, if two random variables following a normal distribution are independent, the joint distribution for the squared values of each variable can be said to follow a chi-square distribution with 2 degrees of freedom.

The probability density function of the standard chi-square distribution is as Equation 6.

$$\begin{align}\tag{6} &f(x;k)=\frac{x^{\frac{k}{2}-1} e^{-\frac{x}{2}}}{2^{\frac{k}{2}}\Gamma(\frac{k}{2})}\\ &\text{degree of freedom}: k>0\\ & x>0 \end{align}$$

As shown in Equation 6, the shape of the chi-square distribution depends on the degrees of freedom (k), so k is called shape parameter. This probability density function is calculated using scipy.stats.chi.pdf().

Figure 3 shows the change in distribution according to degrees of freedom.

plt.figure(figsize=(7, 4))
k=[1, 2, 5, 8, 10]
col=['black', 'blue', 'red', 'green', 'gray']
for i, j in zip(k, col):
    x=np.linspace(stats.chi.ppf(0.01, 5), stats.chi.ppf(0.99, 5),100)
    plt.plot(x, stats.chi.pdf(x, i), color=j, label="k: "+str(i))
plt.legend(loc="best")
plt.ylim(0,1)
plt.xlabel("x", fontsize="13", fontweight="bold")
plt.ylabel("pdf", fontsize="13", fontweight="bold")
plt.title(r"$\chi^2$ distribution by degrees of freedom", fontsize="14", fontweight="bold")
plt.show()

Figure 3. Effect of $\alpha$ and $\lambda$ on gamma distribution.

As shown in Figure 3, the chi-square distribution is not symmetrical unlike the normal distribution, but as k increases, it becomes closer to the normal distribution.

Example 3)
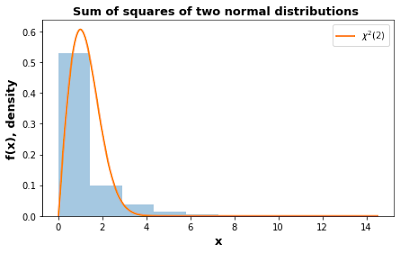
  It shows that the joint distribution for the sum of squares of two independent normal distributions becomes a chi-square distribution.

x=stats.norm.rvs(size=1000)
y=stats.norm.rvs(size=900)
z=np.append(x**2, y**2)
z1=np.sort(z)
plt.figure(figsize=(7,4))
plt.hist(z1, bins=10, density=True, alpha=0.4)
plt.plot(z1, stats.chi.pdf(z1, 2),linewidth=2, label=r"$\chi^2(2)$")
plt.xlabel("x", fontsize="13", fontweight="bold")
plt.ylabel("f(x), density", fontsize="13", fontweight="bold")
plt.legend(loc="best")
plt.title("Sum of squares of two normal distributions ", fontsize="13", fontweight="bold")
plt.show()

Figure 4.

The mean and variance of this distribution are given in Equation 7.

$$\begin{align}\tag{7} E(X)&=\int^\infty_0 x\cdot f(x) \, dx \\&=k\\ E(X^2)&=\int^\infty_0 x^2\cdot f(x) \, dx \\&=k(k+2)\\ Var(X)&=E(X^2)-(E(X))^2\\&=2k\\ \end{align}$$

x,k=symbols("x, k", positive=True)
f=(x**(k/2-1)*exp(-x/2))/(2**(k/2)*gamma(k/2))
f

$\qquad \color{blue}{\displaystyle \frac{2^{- \frac{k}{2}} x^{\frac{k}{2} - 1} e^{- \frac{x}{2}}}{\Gamma\left(\frac{k}{2}\right)}}$

E=integrate(x*f, (x, 0, oo))
simplify(E)

k

E2=integrate(x**2*f,(x,0, oo))
simplify(E2)

k(k+2)

var=E2-(E)**2
simplify(var)

2k

Example 4)
  If the random variable X fits the chi-square distribution with 10 degrees of freedom, what is 95% of the value?

This example determines the random variable x where P(X ≤ x)=0.95. It can be found in the chi-square distribution table. It can be calculated with the scipy.stats.chi2.ppf() method.

round(stats.chi2.ppf(0.95, df=10), 4)

18.307

F distribution

The distribution of the ratio of two random variables ($X_1,\; X_2$) with $k_1$ and $k_2$ degrees of freedom following the chi-square distribution is called the F distribution. A new random variable F is calculated as Equation 8.

$$\begin{equation}\tag{8} F=\frac{X^2_1/k_1}{X^2_2/k_2} \end{equation}$$

As shown in Equation 8, the factor determining the F distribution is two degrees of freedom. If each is expressed as d₁ and d₂, the F distribution is expressed as

$$\text{F} \sim \text{F}(d_1, \; d_2)$$

The probability density function of the random variable x following the F distribution is as Equation 9.

$$\begin{align} \tag{9} f(x)&=\frac{1}{\text{B}(d_1/2, d_2/2)}\left(\frac{d_1x}{d_1x+d_2}\right)^\frac{d_1}{2} \left(1-\frac{d_1x}{d_1x+d_2}\right)^\frac{d_2}{2} x^{-1}\\ &B:\text{Beta function}\\& x \ge 0 \\ & d_1, d_2: \text{positive integer} \end{align}$$

The ratio of the gamma function is: $$\begin{align}B(x, y)&=\frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)}\\ &\int^1_0 t^{x-1}(1-t)^{y-1}\, dt \end{align}$$

Various statistics of the F distribution can be calculated using various methods of the scipy.stats.F class, and the probability density function $^{\ref{fPdf}}$ is typically applied.

Figure 5 shows the change in F distribution according to the numerator and denominator degrees of freedom.

df=[(2, 4),(12,12), (9,9), (4,6)]
rng=np.linspace(0.001, 5, 1000)
for i, j in df:
    x=[stats.f.pdf(k, i, j) for k in rng]
    plt.plot(rng, x, label='F('+str(i)+','+str(j)+')')
plt.legend(loc="best")
plt.xlabel('x', fontsize="13", fontweight="bold")
plt.ylabel('f(x)', fontsize="13", fontweight="bold")
plt.show()

Figure 5. Effect of degrees of freedom on F distribution.

Example 5)
  P(F_6,14 ≤ 1.5)?

round(stats.f.cdf(1.5, 6, 14),4)

0.7515